
����Ŀ����ͼ,�ڱ߳�Ϊ4��������ABCD��,��P��AB�ϴ�A��B�˶�,����DP��AC�ڵ�Q��

��1����֤�������۵�P�˶���AB�Ϻδ�ʱ,������ADQ�ա�ABQ��
��2������P��AB���˶���ʲôλ��ʱ,��ADQ�������������ABCD�����![]() ��
��
��3������P�ӵ�A�˶�����B,�ټ�����BC���˶�����C,�������˶�������,����P�˶���ʲôλ��ʱ,��ADQǡΪ���������Σ�
���𰸡���1��֤������������2��AP=2����3��P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�
��������
�����������1������SAS�����ADQ�ա�ABQ��
��2������Q��QE��AD��E��QF��AB��F����QE=QF������ADQ�������������ABCD�����![]() ������S��ADQ=
������S��ADQ=![]() ADQE=
ADQE=![]() S������ABCD�����OE��ֵ����������DEQ�ס�DAP��
S������ABCD�����OE��ֵ����������DEQ�ס�DAP��![]() �����APֵ��
�����APֵ��
��3����P�˶�ʱ����ADQǡΪ���������ε���������֣���QD=QA��DA=DQ��AQ=AD���������ε�����֪��������P�˶������B�غ�ʱ��QD=QA����ʱ��ADQ�ǵ��������Σ�������P���C�غ�ʱ����Q���CҲ�غϣ���ʱDA=DQ����ADQ�ǵ��������Σ�����AD=AQ=4ʱ����CP=CQ��CP=AC-AD���������εĶԽ��ߵ����ʵõ�CP��ֵ��
�����������1����������ABCD��
���۵�P�˶���AB�Ϻδ�ʱ������
AD=AB����DAQ=��BAQ��AQ=AQ��
���ADQ�ա�ABQ��
��2����ADQ�����ǡ����������ABCD�����![]() ʱ��
ʱ��
����Q��QE��AD��E��QF��AB��F����QE=QF��

���ڱ߳�Ϊ4��������ABCD�У�
��S������ABCD=16��
��![]() AD��QE=
AD��QE=![]() S������ABCD=
S������ABCD=![]() ��16=
��16=![]() ��
��
��QE=![]() ��
��
��EQ��AP��
���DEQ�ס�DAP��
��![]() ����
����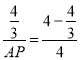 ��
��
���AP=2��
��AP=2ʱ����ADQ�������������ABCD�����![]() ��
��
��3������ADQ�ǵ��������Σ�����QD=QA��DA=DQ��AQ=AD��
����AD=DQʱ������DQA=��DAQ=45��
���ADQ=90����PΪC�㣬
����AQ=DQʱ������DAQ=��ADQ=45����
���AQD=90����PΪB��
��AD=AQ��P��BC�ϣ���
��CQ=AC-AQ=![]() BC-BC=��
BC-BC=��![]() -1��BC
-1��BC
��AD��BC
��![]() �����ɵ�
�����ɵ�![]() =1��
=1��
��CP=CQ=��![]() -1��BC=4��
-1��BC=4��![]() -1��
-1��
���ϣ�P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε�һ�߳�Ϊ4����һ�߳�Ϊ8����������������ε��ܳ�Ϊ �� ��
A. 16 B. 20 C. 20��16 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ���Ϊ( )
������С������������������ѭ��С������������������������������С������������Ҳ�и���������������Ϊ�����������㡢����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϣ���ٷ�չ����ᣬ����Ϣ�������ѳ�Ϊ�����������Ҫ���֣�����������ȡ�˲��ּ�ͥ������ÿ��������Ϣ���ѵĽ�������������ͼ��ʾ�IJ�����ͳ��ͼ����֪A��B���黧��ֱ��ͼ�ĸ߶ȱ�Ϊ1��5������ͼ��������ݻش��������⣺

��1��A���Ƶ���� �����ε��������������� ��
��2����ȫֱ��ͼ�����������Ƶ������
��3������������1500��ס�������������Ϣ���Ѷ����300Ԫ�Ļ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������Գ�ͼ�Σ���Գ�����_______________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ÿ�����ֱ�������Сľ���ij��ȣ��������ܰڳ������ε��ǣ�������
A. 3cm��4cm��8cm B. 8cm��7cm��15cm
C. 13cm��12cm��20cm D. 5cm��5cm��11cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2-2x+1=0 �ĸ������Ϊ�� ��
A. ��������ȵ�ʵ���� B. ����������ȵ�ʵ����
C. ֻ��һ��ʵ���� D. û��ʵ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com