
如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.

(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
科目:初中数学 来源:2016年初中毕业升学考试(陕西卷)数学(解析版) 题型:解答题
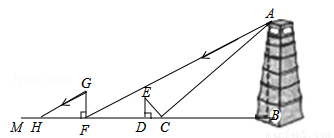
某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(山东东营卷)数学(解析版) 题型:单选题
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
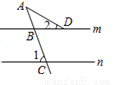
A. 30° B. 35° C. 40° D. 50°
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(宁夏卷)数学(解析版) 题型:选择题
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF= ,BD=2,则菱形ABCD的面积为( )
,BD=2,则菱形ABCD的面积为( )

A.2 B.
B. C.6
C.6 D.8
D.8
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(辽宁沈阳卷)数学(解析版) 题型:解答题
我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
如图,抛物线y=x2﹣3x+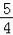 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
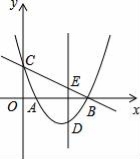
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年河南省濮阳市八年级下期中数学试卷(解析版) 题型:选择题
若 =﹣a成立,则满足的条件是( )
=﹣a成立,则满足的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com