

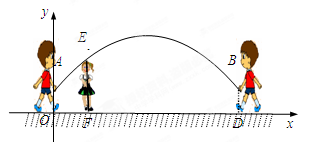
 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.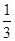 x2﹣2x;
x2﹣2x;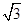 ,﹣1+2
,﹣1+2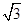 )或(﹣6﹣
)或(﹣6﹣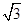 ,﹣1﹣2
,﹣1﹣2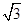 ).
).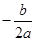 =﹣3,b=6a…①
=﹣3,b=6a…①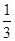 ,b=﹣2,
,b=﹣2,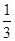 x2﹣2x;
x2﹣2x;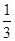 x2﹣2x,
x2﹣2x,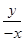 =tan30°=
=tan30°=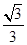 ,
,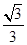 x.
x.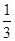 x2﹣2x上,
x2﹣2x上,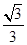 x=﹣
x=﹣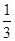 x2﹣2x,
x2﹣2x,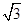 ,x=0(不合题意,舍去)
,x=0(不合题意,舍去)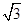 ,﹣1+2
,﹣1+2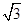 ).
).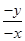 =tan30°=
=tan30°=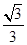 ,
,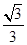 x,
x,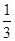 x2﹣2x上.
x2﹣2x上.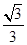 x=﹣
x=﹣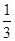 x2﹣2x,
x2﹣2x,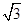 ,x=0(不合题意,舍去).
,x=0(不合题意,舍去).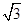 ,﹣1﹣2
,﹣1﹣2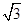 ),
),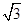 ,﹣1+2
,﹣1+2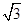 )或(﹣6﹣
)或(﹣6﹣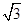 ,﹣1﹣2
,﹣1﹣2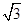 ).
).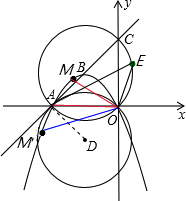 .
.

科目:初中数学 来源:不详 题型:解答题
 ),那么:
),那么:
 ,求
,求 关于
关于 的函数解析式。
的函数解析式。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com