
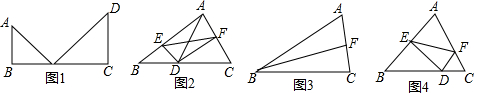
分析 (1)如图1中,作点A关于直线BC的对称点A1,连接DA1交BC于P,连接AP,此时PA+PD最小.作A1E⊥DC于E,在Rt△DEA1中利用勾股定理即可解决问题.
(2)首先证明四边形AEDF是矩形,推出EF=AD,当AD⊥BC时,AD的长最短,求出AD的最小值即可解决问题.
(3)作点F关于直线AB的对称点P,点F关于直线BC的对称点Q,连接PQ交AB于E,交BC于D,连接EF、DF,此时△DEF的周长最小.只要证明△PBQ是等边三角形即可解决问题.
(4)作BF⊥AC于F,作点F关于直线AB的对称点P,点F关于直线BC的对称点Q,连接PQ交AB于E,交BC于D,连接EF、DF,此时△DEF的周长最小.只要证明△PBQ是等腰直角三角形,求出PQ即可解决问题.
解答 解:(1)如图1中,作点A关于直线BC的对称点A1,连接DA1交BC于P,连接AP,此时PA+PD最小.作A1E⊥DC于E,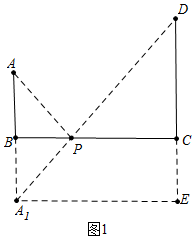
∵∠CBA1=∠BCE=∠E=90°,
∴四边形BCEA1是矩形,
∴AB=BA1=EC=3,
在Rt△EDA1中,∵∠E=90°,EA1=6,DE=8,
∴DA1=$\sqrt{D{E}^{2}+{A}_{1}{E}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴PA+PD的最小值=PA1+PD=DA1=10.
故答案为10.
如图2中,
∵DE⊥AB,DF⊥AC,
∴∠EAF=∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∴EF=AD,
∴当AD⊥BC时,AD的长最短,
∵$\frac{1}{2}$•AB•AC=$\frac{1}{2}$•BC•AD,
∴AD=$\frac{AB•AC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$.
(3)如图3中.
作点F关于直线AB的对称点P,点F关于直线BC的对称点Q,连接PQ交AB于E,交BC于D,连接EF、DF,此时△DEF的周长最小.
∴∠ABP=∠ABF,∠BCF=∠BCQ,BF=BP=BQ,
∵∠ABC=30°,
∴∠PBQ=60°,
∴△PBQ是等边三角形,
∴PQ=PB=BF=4,
∴△DEF的周长的最小值=EF+ED+DQ=PE+ED+DQ=PQ=4.
(4)作BF⊥AC于F,
作点F关于直线AB的对称点P,点F关于直线BC的对称点Q,连接PQ交AB于E,交BC于D,连接EF、DF,此时△DEF的周长最小.
∴∠ABP=∠ABF,∠BCF=∠BCQ,BF=BP=BQ,
∵∠ABC=45
∴∠PBQ=90
∴△PBQ是等腰直角三角形,
在Rt△BCF中,∵∠BFC=90°,BC=2$\sqrt{3}$+2,∠C=60°,
∴∠CBF=30°,
∴CF=$\frac{1}{2}$BC=$\sqrt{3}$+1,BF=$\sqrt{3}$CF=3+$\sqrt{3}$,
在Rt△PBQ中,PQ=$\sqrt{2}$PB=3$\sqrt{2}$+$\sqrt{6}$,
∴△DEF的周长的最小值=EF+DE+DF=PE+DE+DQ=PQ=3$\sqrt{2}$+$\sqrt{6}$.
点评 本题考查三角形综合题、轴对称-最短问题、两点之间线段最短、等边三角形的性质和判定、等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用对称解决最短问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
 (1)阅读理解:
(1)阅读理解:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,且BC∥QR,则∠AOQ的度数为( )
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,且BC∥QR,则∠AOQ的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3$\frac{5}{6}$$<-3\frac{6}{7}$ | B. | -1.38>-1.384 | C. | 4.2>-$\frac{21}{5}$ | D. | -2>-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com