已知在平面直角坐标系xOy中,二次函数y=x2-bx+c(b>0)的图象经过点A(-1,b),与y轴相交于点B,且∠ABO的余切值为3.
(1)求点B的坐标;
(2)求这个函数的解析式;
(3)如果这个函数图象的顶点为C,求证:∠ACB=∠ABO.
分析:(1)根据题意,得b=1+b+c,可得c=-1,从而得出点B的坐标;
(2)过点A作AH⊥y轴,垂足为点H.由∠ABO的余切值为3,∴
cot∠ABO==3,而AH=1,可得BH=3.又BO=1,可得HO=2,b=2,从而得出函数的解析式.
(3)由y=x
2-2x-1=(x-1)
2-2,得顶点C的坐标为(1,-2).根据已知可证明∴△ABC∽△AOB,从而得出∠ACB=∠ABO.
解答: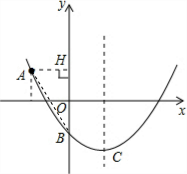
解:(1)根据题意,得b=1+b+c.
∴c=-1.
∴B(0,-1);
(2)过点A作AH⊥y轴,垂足为点H.
∵∠ABO的余切值为3,∴
cot∠ABO==3.
而AH=1,∴BH=3.
∵BO=1,∴HO=2.
∴b=2.
∴所求函数的解析式为y=x
2-2x-1;
(3)由y=x
2-2x-1=(x-1)
2-2,得顶点C的坐标为(1,-2).
∴
AC=2,
AB=,
BC=,
AO=,BO=1.
∴
===.
∴△ABC∽△AOB.
∴∠ACB=∠ABO.
点评:本题考查了二次函数综合题,难度一般,关键是掌握相似三角形的证明方法.

 解:(1)根据题意,得b=1+b+c.
解:(1)根据题意,得b=1+b+c.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.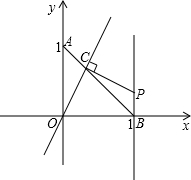 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.