
【题目】从M地到N地有一条普通公路,总路程为120km;有一条高速公路,总路程为126km.甲车和乙车同时从M地开往N地,甲车全程走普通公路,乙车先行驶了另一段普通公路,然后再上高速公路.假设两车在普通公路和高速公路上分别保持匀速行驶,其中在普通公路上的行车速度为60km/h,在高速公路上的行车速度为100km/h.设两车出发x h时,距N地的路程为y km,图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系.
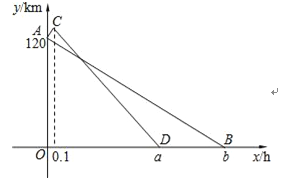
(1)填空:a= ,b= ;
(2)求线段AB、CD所表示的y与x之间的函数关系式;
(3)两车在何时间段内离N地的路程之差达到或超过30km?
【答案】(1)1.36,2;(2)y1=﹣60x+120;y2=﹣100x+136;
(3)当1.15≤x≤1.5时,两车离N地的路程之差达到或超过30km.
【解析】
试题分析:(1)求出C坐标,再根据时间=路程÷速度分别求出甲车在普通公路上行驶的时间及乙车在高速公路上行驶的时间,可得a、b的值;
(2)根据A、B、C、D四点坐标待定系数法求解可得线段AB、CD所表示的y与x之间的函数关系式;
(3)分类讨论:当0<x<0.1时,由解析式可知甲、乙两车距离差最大为12;当0.1≤x<1.36时,由y1﹣y2≥30列不等式可得x的范围;当1.36≤x≤2时,由y1≥30列不等式可得此时x的范围,综合以上三种情况可得答案.
试题解析:(1)根据题意,知:点C的坐标为(0.1,126),
∴a=0.1+![]() =1.36,b=
=1.36,b=![]() =2,
=2,
故答案为:1.36,2.
(2)设线段AB所表示的y与x之间的函数关系式分别为y1=k1x+b1,
将A(0,120)、B(2,0)的坐标代入得:
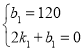 ,
,
解得: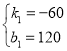 ,
,
∴y1=﹣60x+120;
设线段CD所表示的y与x之间的函数关系式分别为y2=k2x+b2,
将C(0.1,126)、D(1.36,0)的坐标代入得:
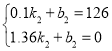 ,
,
解得: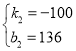 ,
,
∴y2=﹣100x+136.
(3)由题意,①当x=0.1时,两车离N地的路程之差是12km,
∴当0<x<0.1时,两车离N地的路程之差不可能达到或超过30km.
②当0.1≤x<1.36时,由y1﹣y2≥30,得(﹣60x+120)﹣(﹣100x+136)≥30,
解得x≥1.15.
即当1.15≤x<1.36时,两车离N地的路程之差达到或超过30km.
③当1.36≤x≤2时,由y1≥30,得﹣60x+120≥30,解得x≤1.5.
即当1.36≤x≤1.5时,两车离N地的路程之差达到或超过30km.
综上,当1.15≤x≤1.5时,两车离N地的路程之差达到或超过30km.


科目:初中数学 来源: 题型:
【题目】有一个周长为40厘米的正方形,从四个角各剪去一个正方形,做成一个无盖盒子.设这个盒子的底面积为y,剪去的正方形的边长为x,求有关y的二次函数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
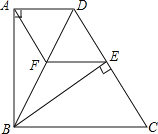
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办中学生足球赛,初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛,六支球队分成甲、乙两组,甲组由A、e、f三队组成,乙组由B、g、h三队组成,现要从甲、乙两组中各随机抽取一支球队进行首场比赛.
(1)在甲组中,首场比赛抽到e队的概率是 ;
(2)请你用画树状图或列表的方法,求首场比赛出场的两个队都是县区学校队的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.

(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com