
【题目】甲、乙二人均从A地出发,甲以60米/分的速度向东匀速行进,10分钟后,乙以(60+m)米/分的速度按同样的路线去追赶甲,乙出发5.5分钟后,甲以原速原路返回,在途中与乙相遇,相遇后两人均停止行进.设乙所用时间为t分钟.
(1)当m=6时,解答:
①设甲与A地的距离为![]() ,分别求甲向东行进及返回过程中,
,分别求甲向东行进及返回过程中,![]() 与t的函数关系式(不写t的取值范围);
与t的函数关系式(不写t的取值范围);
②当甲、乙二人在途中相遇时,求甲行进的总时间.
(2)若乙在出发9分钟内与甲相遇,求m的最小值.
【答案】(1)①甲向东行进过程中,![]() =60t+600;甲返回过程中,
=60t+600;甲返回过程中,![]() =-60t+1260;②甲、乙二人在途中相遇时,甲行进的总时间为20分钟;(2)m的最小值为20.
=-60t+1260;②甲、乙二人在途中相遇时,甲行进的总时间为20分钟;(2)m的最小值为20.
【解析】
(1)①根据题意可得![]() 与t的函数关系式;
与t的函数关系式;
②求出![]() 与t的函数关系式,再结合①的结论列方程解答即可;
与t的函数关系式,再结合①的结论列方程解答即可;
(2)根据题意列不等式解答即可.
(1)①甲向东行进过程中,![]() =60(t+10)=60t+600,
=60(t+10)=60t+600,
t=5.5时,![]() =60t+600=930.
=60t+600=930.
甲返回过程中,![]() =930-60(t-5.5)=-60t+1260.
=930-60(t-5.5)=-60t+1260.
②乙追甲所走的路程![]() =66t,
=66t,
甲、乙二人在途中相遇时,66t=-60t+1260,
解得:t=10,
10+10=20(分),
∴甲、乙二人在途中相遇时,甲行进的总时间为20分钟;
(2)由题意,
得:(60+m)×9+60×(9-5.5)≥930.
解得:m≥20,
∴m的最小值为20.


科目:初中数学 来源: 题型:
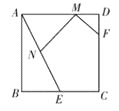
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的课余生活,计划购买排球和篮球供球类兴趣小组活动使用,若购买4个篮球和3个排球需用94元;若购买16个篮球和5个排球需用306元;
(1)求一个篮球和一个排球各多少元;
(2)该中学决定购买排球和篮球共40个,总费用不超过550元,那么该中学至少可以购买多少个排球?
查看答案和解析>>
科目:初中数学 来源: 题型:
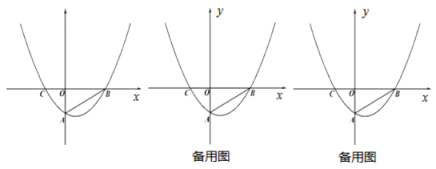
【题目】如图,平面直角坐标系中,抛物线![]() 与
与![]() 轴交于B、C两点(点B在点C右侧),与
轴交于B、C两点(点B在点C右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点P在第二象限的抛物线上,连接PB交![]() 轴于D,取PB的中点E,过点E作
轴于D,取PB的中点E,过点E作![]() 轴于点H,连接DH,设点P的横坐标为
轴于点H,连接DH,设点P的横坐标为![]() .
.![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,作![]() 轴于F,连接CP、CD,
轴于F,连接CP、CD,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,连接BF并延长交抛物线于点
,连接BF并延长交抛物线于点![]() .
.![]() ,在射线CS上取点Q.连接QF,
,在射线CS上取点Q.连接QF,![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
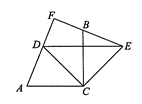
【题目】如图,∠ACB=90°,AC=BC,CD平分∠ACB,点D,E关于CB对称,连接EB并延长,与AD的延长线交于点F,连接DE,CE.对于以下结论:
①DE垂直平分CB;②AD=BE;③∠F不一定是直角;④EF2+DF2=2CD2.
其中正确的是( )
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
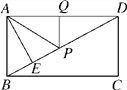
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,DE=3BE,点P,Q分别在BD,AD 上,则AP+PQ的最小值为:
A. 2![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两点(点A在点B的右侧).
轴交于A、B两点(点A在点B的右侧).
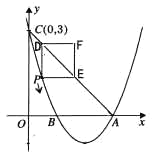
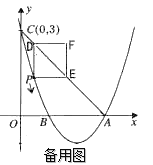
(1)求该抛物线的函数关系式;
(2)点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
(3)在问题(2)的条件下,P点满足∠DAP=90°,且点E在![]() 轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小慧去某风景区游览,两人在景点古刹处碰面,相约一起去游览景点飞瀑,小聪骑自行车先行出发,小慧乘电动车出发,途径草甸游玩后,再乘电动车去飞瀑,结果两人同时到达飞瀑.图中线段![]() 和折线
和折线![]() 表示小聪、小慧离古刹的路程
表示小聪、小慧离古刹的路程![]() (米)与小聪的骑行时间
(米)与小聪的骑行时间![]() (分)的函数关系的图象,根据图中所给信息,解答下列问题:
(分)的函数关系的图象,根据图中所给信息,解答下列问题:
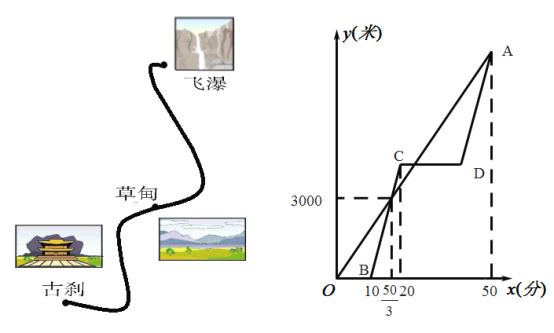
(1)小聪的速度是多少米/分?从古刹到飞瀑的路程是多少米?
(2)当小慧第一次与小聪相遇时,小慧离草甸还有多少米?
(3)在电动车行驶速度不变的条件下,求小慧在草甸游玩的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
(1)①方程![]() 半等分根方程(填“是”或“不是”);
半等分根方程(填“是”或“不是”);
②若![]() 是半等分根方程,则代数式
是半等分根方程,则代数式![]() ;
;
(2)若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是半等分根方程吗?并说明理由;
是半等分根方程吗?并说明理由;
(3)如果方程![]() 是半等分根方程,且相异两点
是半等分根方程,且相异两点![]() ,
,![]() 都在抛物线
都在抛物线![]() 上,试说明方程
上,试说明方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com