
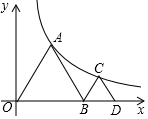
 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$+$\sqrt{6}$ | C. | 3$\sqrt{3}$+2$\sqrt{6}$ | D. | 2$\sqrt{6}$ |
分析 分别过点A、C作x轴的垂线,垂足分别为E、F,设OA=OB=2x,再用x表示出A点坐标,根据锐角三角函数的定义求出BF的长,故可用x表示出a的值,再由AC两点均在反比例函数的图象上求出x的值,进而可得出结论.
解答 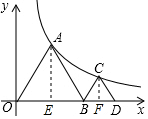 解:如图,分别过点A、C作x轴的垂线,垂足分别为E、F,设OA=OB=2x,
解:如图,分别过点A、C作x轴的垂线,垂足分别为E、F,设OA=OB=2x,
∵△ADB、△BCD均为等边三角形,C(a、$\sqrt{3}$),
∴AE=$\sqrt{3}$x,BF=1,
∴A(x,$\sqrt{3}$x),C(2x+1,$\sqrt{3}$).
∵A、C两点均在反比例函数的图象上,
∴$\sqrt{3}$x2=$\sqrt{3}$(2x+1),解得x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$(不合题意),
∴C(3+2$\sqrt{2}$,$\sqrt{3}$),
∴k=(3+2$\sqrt{2}$)×$\sqrt{3}$=3$\sqrt{3}$+2$\sqrt{6}$.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
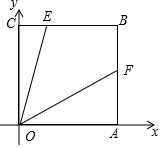 如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )
如图,在正方形OABC中,点B的坐标是(3,3),点E,F分别在边BC,BA上,CE=1,若∠EOF=45°,则F点的纵坐标是( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
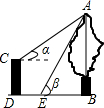 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
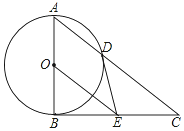 如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
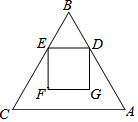 △ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于6$\sqrt{3}$-6.
△ABC是边长为18的正三角形,点D、E分别在边AB、BC上,且BD=BE.若四边形DEFG是边长为6的正方形时,则点F到AC的距离等于6$\sqrt{3}$-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
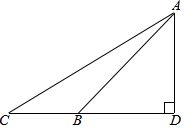 如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com