
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A

(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
(1)证明见解析;(2)60°.
【解析】
试题分析:(1)连结OA、OB、OC、BD,根据切线的性质得OA⊥AB,即∠OAB=90°,再根据菱形的性质得BA=BC,然后根据“SSS”可判断△ABO≌△CBO,则∠BCO=∠BAO=90°,于是可根据切线的判定方法即可得到结论;
(2)由△ABO≌△CBO得∠AOB=∠COB,则∠AOB=∠COB,由于菱形的对角线平分对角,所以点O在BD上,利用三角形外角性质有∠BOC=∠ODC+∠OCD,则∠BOC=2∠ODC,由于CB=CD,则∠OBC=∠ODC,所以∠BOC=2∠OBC,根据∠BOC+∠OBC=90°可计算出∠OBC=30°,然后利用∠ABC=2∠OBC计算即可.
试题解析:(1)连结AO、CO、DO
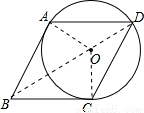
∵AB与⊙O切于A点,
∴OA⊥AB,即∠OAB=90°,
∵四边形ABCD为菱形,
∴BA=BC,
在△ABO和△CBO中
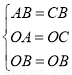 ,
,
∴△ABO≌△CBO(SSS),
∴∠BCO=∠BAO=90°,
∴OC⊥BC,
∴BC为⊙O的切线;
(2)【解析】
∵△ABO≌△CBO,
∴∠ABO=∠CBO,
∵四边形ABCD为菱形,
∴BD平分∠ABC,DA=DC,
∴点O在BD上,
∵∠BOC=∠ODC+∠OCD,
而OD=OC,
∴∠ODC=∠OCD,
∴∠BOC=2∠ODC,
而CB=CD,
∴∠OBC=∠ODC,
∴∠BOC=2∠OBC,
∵∠BOC+∠OBC=90°,
∴∠OBC=30°,
∴∠ABC=2∠OBC=60°.
考点:1.切线的判定与性质;2.菱形的性质.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源:2014-2015学年河南省商丘市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,一段抛物线 记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )
记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷(解析版) 题型:解答题
(本题8分)甲、乙两班学生到集市上购买苹果,苹果的价格如下:

甲班分两次共购买苹果70千克(第二次多于第一次),共付出189元,而乙班则一次购买苹果70千克.
(1)乙班比甲班少付出多少元?
(2)甲班第一次、第二次分别购买多少千克?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷(解析版) 题型:选择题
已知∠AOB=80°,以0为顶点,OB为一边作∠BOC=20°,则∠AOC的度数为( ).
A.100° B.60° C.100°或60° D.80°或20°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷(解析版) 题型:选择题
已知太阳的半径约为696000000m,则696000000这个数用科学记数法可表示为 ( ).
A.0.696×109 B.6.96×109
C.6.96×108 D.69.6×107
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省三门峡市九年级上学期期末考试数学试卷(解析版) 题型:选择题
抛物线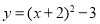 可以由抛物线y=x2平移得到,则下列平移过正确的是( )
可以由抛物线y=x2平移得到,则下列平移过正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市房山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省祁阳县九年级下学期期末教学质量检测数学试卷(解析版) 题型:选择题
若点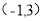 ,
,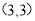 是二次函数
是二次函数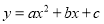 图象上的两点,则此二次函数的对称轴是( )
图象上的两点,则此二次函数的对称轴是( )
A.直线x=-1 B.直线
C.直线x=1 D.直线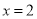
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com