练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图16，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y=+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是________.

    【答案】-2＜k＜．

    【解析】由图可知，∠AOB=45°，∴直线OA的解析式为y=x，联立 ，消掉y得，x2﹣2x+2k=0，△=b2﹣4ac=（﹣2）2﹣4×1×2k=0，即k= 时，抛物线与OA有一个交点，此交点的横坐标为1，∵点B的坐标为（2，0），∴OA=2，∴点A的坐标为（， ），∴交点在线段AO上；当抛物线经过点B（2，0）时， ×4+k=0，解得k=﹣2，∴要使抛物线y= x2+k与扇形OAB的边界总有两个公共点，实数k的取值范围是﹣2＜k＜ ．故答案为： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：|a﹣2|+（b+1）2=0，求2ab2﹣a2b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算0.78×102016﹣4.2×102015的结果用科学记数法可表示为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为正，求实数m的取值范围？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：m，x，y满足：（1）；（2）﹣2a2by+1与7b3a2是同类项．

    求代数式：2x2﹣6y2+m（xy﹣9y2）﹣（3x2﹣3xy+7y2）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正多边形的一个外角等于60°，则该正多边形的边数为(　　)

    A. 3 B. 4 C. 5 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝2（x﹣1）2﹣5的顶点坐标是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某车间有16名工人，每人每天可加工甲种零件5个或乙种零件4个．在这16名工人中，一部分人加工甲种零件，其余的加工乙种零件．已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元．若此车间一共获利1440元，求这一天有几个工人加工甲种零件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

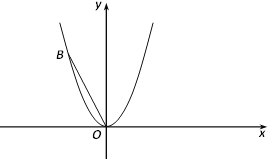
    【题目】如图，平面直角坐标系xOy中，抛物线经过点B(－2，4)．

    （1）求a的值；

    （2）作Rt△OAB，使∠BOA＝90°，且OB＝2OA，求点A坐标；

    （3）在（2）的条件下，过点A作直线AC⊥x轴于点C，交抛物线于点D，将该抛物线向左或向右平移t（t＞0）个单位长度，记平移后点D的对应点为D′，点B的对应点为B′．当CD′＋OB′的值最小时，请直接写出t的值和平移后相应的抛物线解析式．

    查看答案和解析>>

    同步练习册答案