
【题目】如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
(1)指出这个过程中的旋转中心,并说明旋转角度数是多少;
(2)指出图中的对应线段;
(3)连接BD,BF,DF,判断△DBF的形状,并说明理由.
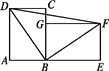
【答案】(1)旋转中心为点B,旋转角度数是90°;(2)对应线段:AB与GB,AD与GF,DC与FE,BC与BE;(3)△DBF是等腰直角三角形,理由见解析.
【解析】试题分析:(1)由长方形的性质得出∠ABC=90°,由已知条件和旋转的性质得出∠CBE=180°-90°=90°,得出旋转中心是点B,旋转角度数是90°;
(2)由旋转的性质得出长方形GBEF≌长方形ABCD,得出BG=BA,BE=BC,EF=CD,GF=AD,即可得出结果;
(3)由旋转的性质得:BF=BD,∠DBF=∠CBE=90°,即可得出结论.
试题解析:(1)∵四边形ABCD是长方形,
∴∠ABC=90°,
∵把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上,
∴∠CBE=180°-90°=90°,
∴旋转中心是点B,旋转角度数是90°;
(2)由旋转的性质得:长方形GBEF≌长方形ABCD,
∴BG=BA,BE=BC,EF=CD,GF=AD,BF=BD,
∴图中的对应线段为BG和BA,BE和BC,EF和CD,GF和AD,BF和BD;
(3)△DBF是等腰直角三角形;理由如下:
由旋转的性质得:BF=BD,∠DBF=∠CBE=90°,
∴△DBF是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线 ![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 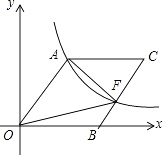
A.60
B.80
C.30
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB=2∠B,∠C=90°,AD为∠BAC的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)



(2)如图2,当∠C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.
(3)如图3,当∠ACB≠90°,∠ACB=2∠B ,AD为△ABC的外角∠CAF的平分线,交BC的延长线于点D,则线段 AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,求大楼AB的高度是多少?(精确到0.1米,参考数据:
,求大楼AB的高度是多少?(精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.45)
≈2.45)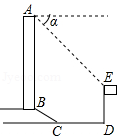
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com