
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

【答案】 7 9 19 39 4 9 16 10000
【解析】
(1)由图中信息可知第4层有7个点;
(2)观察图形中各层点的个数可知,从第一层到第n层点的个数依次是从1开始的连续奇数1、3、5、……,由此可知第n层的点的个数为:(2n-1)个,从而可计算出第五层和第十层的点的个数;
(3)根据(2)中所得结论可得2n-1=77,解此方程即可求得对应的n的值;
(4)由图中信息可得第一层点的个数和第二层点的个数的和为4,前三层点的个数之和为9,前四层点的个数之和为16;由此可得规律为:前n层的点的个数之和为![]() ;由此可得前100层的点的个数之和为:
;由此可得前100层的点的个数之和为:![]() 个.
个.
(1)如图所示:第四层有7个点;
(2)∵第一层有1个点,第二层有3个点,第三层有5个点,第四层有7个点,
∴从第一层到第n层点的个数依次是从1开始的连续奇数1、3、5、……,由此可知第n层的点的个数为:(2n-1)个,
∴如果继续画下去,那么第五层有9个点,第十层有19个点;
(3)某一层上有77个点,即:2n-1=77,解得:n=39,
∴这是第三十九层;
(4)∵第一层与第二层点的个数之和是4=22,前三层点的个数的和是9=32,前四层点的个数的和是16=42,…,
由此可得:前n层的点的个数的和是n2,
∴前一百层的点的个数的和是1002=10000.


科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
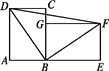
【题目】如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
(1)指出这个过程中的旋转中心,并说明旋转角度数是多少;
(2)指出图中的对应线段;
(3)连接BD,BF,DF,判断△DBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
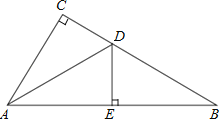
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究,以下是探究发现运用过程,请补充完整.
(1)操作发现,在作函数y=|x|的图象时,采用了分段函数的办法,该函数转化为y= ![]() ,请在如图1所示的平面直角坐标系中作出函数的图象;
,请在如图1所示的平面直角坐标系中作出函数的图象;
(2)类比探究
作函数y=|x﹣1|的图象,可以转化为分段函数 , 然后分别作出两段函数的图象.聪明的小昕,利用坐标平面上的轴对称知识,把函数y=x﹣1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x﹣1|的图象,如图所示;
(3)拓展提高
如图2右图是函数y=x2﹣2x﹣3的图象,请在原坐标系作函数y=|x2﹣2x﹣3|的图象;
(4)实际运用
①函数 ![]() 的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
②函数 ![]() 的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
③函数 ![]() 的图象与直线y=4有个交点,对应方程
的图象与直线y=4有个交点,对应方程 ![]() 有个实根;
有个实根;
④关于x的方程 ![]() 有4个实根时,a的取值范围是 .
有4个实根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
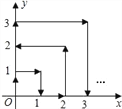
【题目】如图所示一个质点在第一象限内及x轴、y轴上运动,在第一秒内它由原点移动到(0,1)点,而后接着按图所示在x轴,y轴平行的方向运动,且每秒移动一个单位长度,那么质点运动到点(n,n)(n为正整数)的位置时,用代数式表示所用的时间为_________秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 . 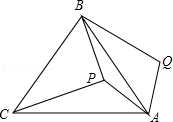
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.4个结论中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com