
 根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号).
根据有理数a,b在数轴上的位置(如图),则有下列六个不等式:①a-b>0;②a+b<0;③ab<0;④b2-a2>0;⑤$\frac{1}{a}$-$\frac{1}{b}$<0;⑥|a|-|b|>0,其中错误的是②③④⑥(只填序号). 分析 根据数轴可得a<0,b>0,|a|>|b|,再根据有理数的加减乘除法则分别进行分析即可.
解答  解:由图可知:a<0,b>0,|a|>|b|,
解:由图可知:a<0,b>0,|a|>|b|,
①a-b>0错误,应为a-b<0,故错误;
②a<0,b>0,|a|>|b|,则a+b<0,故正确;
③a<0,b>0,则ab<0,故正确;
④|a|>|b|,则b2-a2<0,故错误;
⑤|a|>|b|,则$\frac{1}{a}$<0<$\frac{1}{b}$,$\frac{1}{a}$-$\frac{1}{b}$<0,故正确;
⑥|a|>|b|,则|a|-|b|>0,故正确;
综上所述,正确的是②③④⑥.
故答案是:②③④⑥.
点评 此题主要考查了数轴,关键是掌握数轴上的数,负数在原点左边,正数在原点右边.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
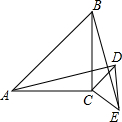 如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.
如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com