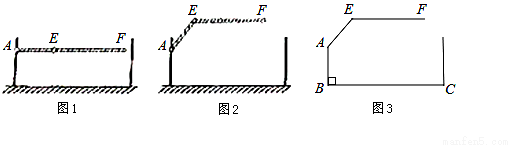
某地下车库出口处“两段式栏杆”如图1所示，点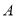
是栏杆转动的支点，点
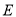是栏杆两段的连接点．当车辆经过时，栏杆
升起后的位置如图2所示，其示意图如图3所示，其中
⊥
， 
∥
，
，
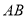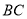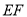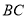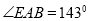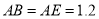米，求当车辆经过时，栏杆EF段距离地面的高度（即直线EF上任意一点到直线BC的距离）．（结果精确到0．1米，栏杆宽度忽略不计参考数据：sin 37° ≈ 0．60，cos 37° ≈ 0．80，tan 37° ≈ 0．75．）
科目：初中数学 来源：2014-2015学年北京市八年级下学期期中数学试卷（解析版） 题型：填空题
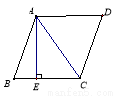
如图，在菱形ABCD中，AB=5，对角线AC=6，若过点A作AE⊥BC，垂足为E，则AE的长为_______.
查看答案和解析>>
科目：初中数学 来源：2014-2015学年辽宁盘锦市中考模拟一数学试卷（解析版） 题型：解答题
（12分）草梅是我地区的特色时令水果，草梅一上市，水果店的老板用1200元购进一批草梅很
快售完；老板又用2500元购进第二批草梅，所购箱数是第一批的2倍，但进价比第一批每箱多了5元．
（1）第一批草梅每箱进价多少元？
（2）老板以每箱150元的价格销售第二批草梅，售出80%后，为了尽快售完，决定打折促销，要使第二批草梅的销售利润不少于320元，剩余的草梅每箱售价至少打几折？ （利润=售价﹣进价）
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省宁波市毕业生学业诊断性考试数学试卷（解析版） 题型：解答题
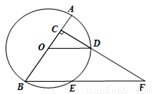
如图，已知AB是⊙O的直径，AB=8， 点C在半径OA上（点C与点O、A不重合），过点C作AB的垂线交⊙O于点D，连结OD，过点B作OD的平行线交⊙O于点E、交射线CD于点F．
（1）若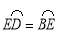
，求∠F的度数；
（2）设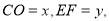
写出
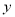与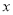
之间的函数解析式，并写出自变量取值范围；
（3）设点C关于直线OD的对称点为P，若△PBE为等腰三角形，求OC的长．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省宁波市毕业生学业诊断性考试数学试卷（解析版） 题型：填空题
若实数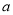
、
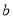满足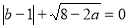
，且一元二次方程kx2+ax+b =0有两个实数根，则k的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省宁波市毕业生学业诊断性考试数学试卷（解析版） 题型：选择题
一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此圆锥的底面半径为（ ）
A．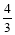
cm B．
cm C． 3cm D．
cm
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省毕业生学业考试数学试卷（解析版） 题型：填空题
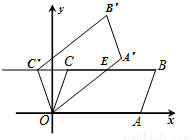
如图，在平面直角坐标系xOy中，□OABC的顶点A、B的坐标分别为（6，0）、（7，3），将□OABC绕点O逆时针方向旋转得到□O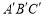
，当点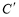
落在BC的延长线上时，线段
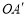交BC于点E，则线段
的长度为 ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省龙口市五中初中毕业班下学期期中考试数学试卷（解析版） 题型：解答题
（10分）（1）如图1，已知△ABC，以AB，AC为边向△ABC外做等边△ABD和等边△ACE．连接BE，CD．请你完成图形，并证明：BE=CD；（尺规作图，不写做法，保留作图痕迹）
（2）如图2，已知△ABC，以AB，AC为边向外做正方形ABFD和正方形ACGE．连接BE，CD．BE与CD有什么数量关系？简单说明理由．
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC＝45°，∠CAE＝90°，AB＝BC＝10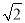
米，AC＝AE．求BE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B．
C．
D．