
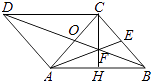
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
【答案】
(1)解:如图,连接BD,BD与AE交于点F,连接CF并延长到AB,则它与AB的交点即为H.
理由如下:
∵BD、AC是ABCD的对角线,
∴点O是AC的中点,
∵AE、BO是等腰△ABC两腰上的中线,
∴AE=BO,AO=BE,
∵AO=BE,
∴△ABO≌△BAE(SSS),
∴∠ABO=∠BAE,
△ABF中,∵∠FAB=∠FBA,∴FA=FB,
∵∠BAC=∠ABC,
∴∠EAC=∠OBC,
由 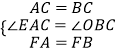 可得△AFC≌BFC(SAS)
可得△AFC≌BFC(SAS)
∴∠ACF=∠BCF,即CH是等腰△ABC顶角平分线,
所以CH是△ABC的高;
(2)解:∵AC=BC=5,AB=6,CH⊥AB,
∴AH= ![]() AB=3,
AB=3,
∴CH= ![]() =4,
=4,
∴S△ABC= ![]() ABCH=
ABCH= ![]() ×6×4=12,
×6×4=12,
∵AE是△ABC的中线,
∴S△ACE= ![]() S△ABC=6.
S△ABC=6.
【解析】此题考查了平行四边形的性质、等腰三角形的性质、勾股定理以及三角形中线的性质.注意三角形的中线把三角形分成面积相等的两部分.(1)连接BD,BD与AE交于点F,连接CF并延长到AB,与AB交于点H,则CH为△ABC的高;(2)首先由三线合一,求得AH的长,再由勾股定理求得CH的长,继而求得△ABC的面积,又由AE是△ABC的中线,求得△ACE的面积.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn= ![]() (n2﹣an+b)(其中a,b是常数,n≥4)
(n2﹣an+b)(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5=
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣2x+4与平面直角坐标系中的x轴、y轴分别交于A、B两点,以AB为边作等腰直角三角形ABC,使得点C与原点O在AB两侧,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )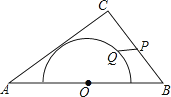
A.6
B.2 ![]() +1
+1
C.9
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺序通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com