
【题目】如图所示,△ABC是等边三角形,D、E分别是BC、AC上一点,且AE=CD,AD,AD、BE交于P,过B作BQ⊥AD于Q,若QP=3cm,PE=1cm,求AD的长。

【答案】7cm
【解析】
根据题意通过“边角边”证明△BAE≌△ACD,得到BE=AD,∠DAC=∠EBA,根据三角形外角的性质求得∠BPQ=60°,然后在Rt△BQP中,求得BP的长,则根据AD=BE=BP+PE即可得到答案.
解:∵△ABC是等边三角形,
∴∠BAC=∠C=60°,AB=AC,
又∵AE=CD,
∴△BAE≌△ACD(SAS),
∴BE=AD,∠DAC=∠EBA,
∴∠BPQ=∠EBA+∠BAP=∠DAC +∠BAP=60°,
又∵BQ⊥AD,
∴∠BQP=90°,
∴∠QBP=30°,
∴QP=![]() BP,
BP,
∵QP=3,
∴BP=6,
∵PE=1,
∴AD=BE=BP+PE=6+1=7.
答:AD的长为7cm.


科目:初中数学 来源: 题型:
【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD= ![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC, ∠C=30°,AB的垂直平分线交BC于E,则下列结论正确的是( )

A. BE=![]() CE B. BE=
CE B. BE=![]() CE C. BE=
CE C. BE= ![]() CE D. 不能确定
CE D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ![]() ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 ![]() CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).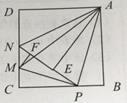
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当 ![]() ABP≌
ABP≌ ![]() AND时,BP=4
AND时,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB, 
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二  找出图中与AB相等的线段,并证明.
找出图中与AB相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个人做游戏:在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.从中随机摸出一张纸牌然后放回,再随机摸出一张纸牌,若两次摸出的纸牌上数字之和是3的倍数,则甲胜;否则乙胜.这个游戏对双方公平吗?请列表格或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
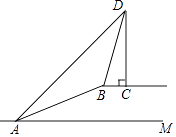
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com