
分析 (1)根据特殊角的三角函数值进行计算即可;
(2)根据特殊角的三角函数值和算术平方根进行计算即可;
(3)根据特殊角的三角函数值和绝对值进行计算即可;
(4)根据特殊角的三角函数值进行计算即可.
解答 解:(1)原式=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$
=$\frac{\sqrt{3}-1}{2}$;
(2)原式=$\sqrt{1-(\frac{\sqrt{2}}{2})^{2}}$-$\sqrt{1-(\frac{\sqrt{3}}{2})^{2}}$
=$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$
=$\frac{\sqrt{2}-1}{2}$;
(3)原式=|$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$|
=$\frac{\sqrt{3}-1}{2}$;
(4)原式=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}$-$\frac{\frac{1}{2}}{1+\frac{1}{2}}$-3×$\frac{\sqrt{3}}{3}$
=1-$\frac{1}{3}$-$\sqrt{3}$
=$\frac{2}{3}$-$\sqrt{3}$.
点评 本题考查了实数的运算,以及特殊角的三角函数值,掌握实数的运算法则以及特殊角的三角函数值、绝对值的计算是解题的关键.


科目:初中数学 来源: 题型:解答题
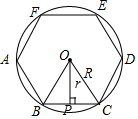 三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积?
三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
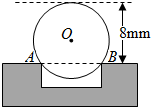 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从5x=x-3得5x-x=-3 | B. | 从7+x=3得x=3+7 | ||
| C. | 从2x+3-x=7得2x+x=7-3 | D. | 从2x-3=x+6得2x+x=6+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,如图,P为△ABC中线AD上一点,AP:PD=2:1,延长BP、CP分别交AC、AB于点E、F,EF交AD于点Q.
已知,如图,P为△ABC中线AD上一点,AP:PD=2:1,延长BP、CP分别交AC、AB于点E、F,EF交AD于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com