Question

12．如图，是一副学生用的三角板，在△ABC 中，∠C=90°，∠A=60°，∠B=30°；在△A₁B₁C₁中，∠C₁=90°，∠A₁=45°，∠B₁=45°，且A₁B₁=CB．若将边A₁C₁与边CA重合，其中点A₁与点C重合．将三角板A₁B₁C₁绕点C（A₁）按逆时针方向旋转，旋转过的角为α，旋转过程中边A₁C₁与边AB的交点为M，设AC=a．
（1）计算A₁C₁的长；
（2）当α=30°时，证明：B₁C₁∥AB；
（3）若a=$\sqrt{6}+\sqrt{2}$，当α=45°时，计算两个三角板重叠部分图形的面积；
（4）当α=60°时，用含a的代数式表示两个三角板重叠部分图形的面积．
（参考数据：sin15°=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$，cos15°=$\frac{{\sqrt{6}+\sqrt{2}}}{4}$，tan15°=2-$\sqrt{3}$，sin75°=$\frac{{\sqrt{6}+\sqrt{2}}}{4}$，cos75°=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$，tan75°=2+$\sqrt{3}$）

Answer 1

分析 （1）在Rt△ABC中，由特殊锐角三角函数值，先求得BC的长，然后在Rt△A₁B₁C₁中利用特殊锐角三角函数即可求得A₁C₁的长；
（2）利用三角形的外角的性质求得∠BMC=90°，然后利用同位角相等，两直线平行进行判定即可；
（3）两个三角板重叠部分图形的面积=△A₁B₁C₁的面积-△BC₁M的面积；
（4）两个三角板重叠部分图形的面积=△CC₁B₁的面积-三角形FB₁C的面积-三角形DC₁M的面积．

解答 解：（1）在Rt△ABC中，∠B=30°，AC=a，
由特殊锐角三角函数可知：$\frac{AC}{BC}=tan30°=\frac{\sqrt{3}}{3}$，
∴BC=$\sqrt{3}a$．
∴B₁C=$\sqrt{3}a$
在Rt△A₁B₁C₁，∠B₁=∠45°，
∴$\frac{{A}_{1}{C}_{1}}{{B}_{1}C}=\frac{\sqrt{2}}{2}$．
∴A₁C₁=$\frac{\sqrt{2}}{2}×\sqrt{3}a$=$\frac{\sqrt{6}a}{2}$．
（2）∵∠ACM=30°，∠A=60°，
∴∠BMC=90°．
∴∠C₁=∠BMC．
∴B₁C₁∥AB．
（3）如下图：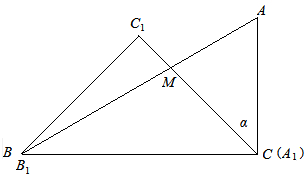

由（1）可知：A₁C₁=$\frac{\sqrt{6}a}{2}$=$\frac{\sqrt{6}}{2}×（\sqrt{6}+\sqrt{2}）$=3+$\sqrt{3}$
∴△A₁B₁C₁的面积=$\frac{1}{2}{B}_{1}{C}_{1}•{C}_{1}{A}_{1}$=$\frac{1}{2}（3+\sqrt{3}）^{2}=6+3\sqrt{3}$
∵∠A₁B₁C₁=45°，∠ABC=30°
∴∠MBC₁=15°
在Rt△BC₁M中，C₁M=BCtan15°=（3+$\sqrt{3}$）（2-$\sqrt{3}$）=3-$\sqrt{3}$，
∴Rt△BC₁M的面积=$\frac{1}{2}{B}_{1}{C}_{1}•{C}_{1}M$=$\frac{1}{2}（3+\sqrt{3}）（3-\sqrt{3}）$=3．
∴两个三角板重叠部分图形的面积=△A₁B₁C₁的面积-△BC₁M的面积=3$\sqrt{3}$+3．
（4）由（1）可知：BC=$\sqrt{3}a$，A₁C₁=$\frac{\sqrt{6}}{2}a$，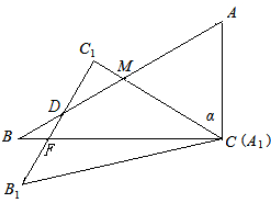
∴C₁F=A₁C₁•tan30°=$\frac{\sqrt{2}}{2}$a，
∴${S}_{△{A}_{1}{C}_{1}F}$=$\frac{1}{2}{A}_{1}{C}_{1}•{C}_{1}F$=$\frac{1}{2}$×$\frac{\sqrt{6}}{2}$a×$\frac{\sqrt{2}}{2}$a=$\frac{\sqrt{3}}{4}$a²，
∵∠MCA=60°，∠A=60°，
∴∠AMC=60°
∴MC=AC=MA=a．
∴C₁M=C₁A₁-MC=$\frac{\sqrt{6}-2}{2}a$．
∵∠MCA=60°，
∴∠C₁A₁B=30°，
∴∠C₁MD=∠B+∠C₁A₁B=60°
在Rt△DC₁M中，由特殊锐角三角函数可知：C₁D=C₁M•tan60°=$\frac{3\sqrt{2}-2\sqrt{3}}{2}$a，
∴${S}_{△D{C}_{1}M}$=$\frac{1}{2}•$C₁M•C₁D₌$\frac{5\sqrt{3}-6\sqrt{2}}{4}$a²，
两个三角板重叠部分图形的面积=${S}_{△{A}_{1}{C}_{1}F}$-${S}_{△D{C}_{1}M}$=$\frac{1}{2}•$C₁M=$\frac{\sqrt{3}}{4}$a²-$\frac{5\sqrt{3}-6\sqrt{2}}{4}$a²=$\frac{3\sqrt{2}-2\sqrt{3}}{2}$a²．

点评 本题主要考查的是锐角三角函数和三角形的综合应用，难度较大，解答本题的关键是灵活应用锐角函数求得相关线段的长度．