

| A.5对 | B.6对 | C.7对 | D.8对 |
 BC=
BC= AB=
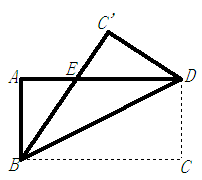
AB= AC,因为∠EDF=60°AE=AF,所以△DEF和△AEF为等边三角形,所以∠EDA=∠FDA=30°,因为∠BAD=∠CAD=30°,所以△ADE和△ADF为等腰三角形,易知△BED≌△DEF≌△CDF≌△AEF, △AED≌△AFD,前者有6对,共7对.
AC,因为∠EDF=60°AE=AF,所以△DEF和△AEF为等边三角形,所以∠EDA=∠FDA=30°,因为∠BAD=∠CAD=30°,所以△ADE和△ADF为等腰三角形,易知△BED≌△DEF≌△CDF≌△AEF, △AED≌△AFD,前者有6对,共7对. BC=
BC= AB=
AB= AC,因为∠EDF=60°AE=AF,所以△DEF和△AEF为等边三角形,所以∠EDA=∠FDA=30°,因为∠BAD=∠CAD=30°,所以△ADE和△ADF为等腰三角形,易知△BED≌△DEF≌△CDF≌△AEF, △AED≌△AFD,前者有6对,共7对.
AC,因为∠EDF=60°AE=AF,所以△DEF和△AEF为等边三角形,所以∠EDA=∠FDA=30°,因为∠BAD=∠CAD=30°,所以△ADE和△ADF为等腰三角形,易知△BED≌△DEF≌△CDF≌△AEF, △AED≌△AFD,前者有6对,共7对.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.点F在BC边的垂直平分线上 | B.点F在∠BAC的平分线上 |
| C.△BCF是等腰三角形 | D.△BCF是直角三角形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com