
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1�����A����B����C�����ꣻ
��2����ֱ��BD�Ľ���ʽ��
��3������P���߶�OB���˶�ʱ��ֱ��l��BD�ڵ�M����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ�
��4���ڵ�P���˶������У��Ƿ���ڵ�Q��ʹ��BDQ����BDΪֱ�DZߵ�ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵��������

���𰸡���1��A����1��0����B��4��0����C��0��2������2��![]() ����3��m=2����4��Q������Ϊ��3��2������8����18��������1��0����
����3��m=2����4��Q��������3��2������8����18��������1��0����
��������
�����������1�����ݺ�������ʽ�з��̼��ɵõ����ۣ�
��2���ɵ�C���D����x��Գƣ��õ�D��0����2�����ⷽ�̼��ɵõ����ۣ�
��3����ͼ1��ʾ������ƽ���ı��ε����ʵõ�QM=CD�����Q������Ϊ��m��![]() ������M��m��
������M��m��![]() �����з��̼��ɵõ����ۣ�
�����з��̼��ɵõ����ۣ�
��4�����Q������Ϊ��m��![]() ����������������ٵ���QBD=90��ʱ�����ݹ��ɶ����з������m=3��m=4���������⣬��ȥ�����ڵ���QDB=90��ʱ�����ݹ��ɶ����з������m=8��m=��1�����ǵõ����ۣ�
����������������ٵ���QBD=90��ʱ�����ݹ��ɶ����з������m=3��m=4���������⣬��ȥ�����ڵ���QDB=90��ʱ�����ݹ��ɶ����з������m=8��m=��1�����ǵõ����ۣ�
�����������1������x=0�ã�y=2����C��0��2����
����y=0�ã�![]() ����ã�
����ã�![]() ��
��![]() ����A����1��0����B��4��0����
����A����1��0����B��4��0����
��2���ߵ�C���D����x��Գƣ���D��0����2����
��ֱ��BD�Ľ���ʽΪy=kx��2��
�߽���4��0������ã�4k��2=0����k=![]() ����ֱ��BD�Ľ���ʽΪ
����ֱ��BD�Ľ���ʽΪ![]() ��
��
��3����ͼ1��ʾ��
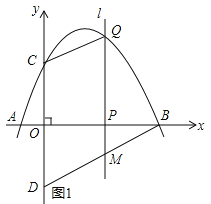
��QM��DC���൱QM=CDʱ���ı���CQMD��ƽ���ı��Σ�
���Q��������m��![]() ������M��m��
������M��m��![]() ������
������![]() ����ã�m=2��m=0���������⣬��ȥ�����൱m=2ʱ���ı���CQMD��ƽ���ı��Σ�
����ã�m=2��m=0���������⣬��ȥ�����൱m=2ʱ���ı���CQMD��ƽ���ı��Σ�
��4�����ڣ����Q������Ϊ��m��![]() �����ߡ�BDQ����BDΪֱ�DZߵ�ֱ�������Σ���������������ۣ�
�����ߡ�BDQ����BDΪֱ�DZߵ�ֱ�������Σ���������������ۣ�
�ٵ���QBD=90��ʱ���ɹ��ɶ����ã�![]() ����
����![]() ����ã�m=3��m=4���������⣬��ȥ������Q��3��2����
����ã�m=3��m=4���������⣬��ȥ������Q��3��2����
�ڵ���QDB=90��ʱ���ɹ��ɶ����ã�![]() ����
����![]() ����ã�m=8��m=��1����Q��8����18��������1��0����
����ã�m=8��m=��1����Q��8����18��������1��0����
������������Q��������3��2������8����18��������1��0����


 �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д� ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EΪ����ֱ����ABC�ı�AB�ϵ�һ�㣬ҪʹAE��3��BE��1��PΪAC�ϵĶ��㣬��PB��PE����СֵΪ____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
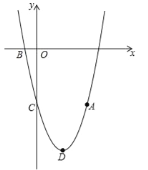
����Ŀ����ͼ��������![]() ��a��0��������A��4����5������x��ĸ����ύ�ڵ�B����y�ύ�ڵ�C����OC=5OB�������ߵĶ���Ϊ��D��
��a��0��������A��4����5������x��ĸ����ύ�ڵ�B����y�ύ�ڵ�C����OC=5OB�������ߵĶ���Ϊ��D��
��1�������������ߵı���ʽ��
��2������AB��BC��CD��DA�����ı���ABCD�������
��3�������E��y����������ϣ��ҡ�BEO=��ABC�����E��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩƷ˵�����ϱ���ҩƷ������¶���(10��4) ��,���ҩƷ���ʵı����¶�Ϊt ��,��t��ȡֵ��Χ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ˮ��˾�����±���ȡˮ��:��ÿ��ÿ����ˮ������10 m3,��ÿ�������շ�1.5Ԫ;��ÿ��ÿ����ˮ����10 m3,������ÿ�������շ�2Ԫ.С����ij�µ�ˮ�Ѳ�����25Ԫ,��ô��������µ���ˮ��x(m3)�����Ƕ���?���г�����x�IJ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������εı߳��������2cm�����������32cm2������������εı߳�Ϊ�� ��
A. 5cm B. 6cm C. 7cm D. 8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x=��1�ǹ���x��һԪ���η���x2��x+c=0��һ��������c��ֵ�ǣ�������
A.2
B.1
C.0
D.-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�����гнӲ�ҵת��ʾ���������Ч���ԣ�һ������ɹ̶��ʲ�Ͷ��238��Ԫ���ÿ�ѧ�������ɼ����� ��
A.238��108ԪB.23.8��109ԪC.2.38��1010ԪD.0.238��1011Ԫ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com