
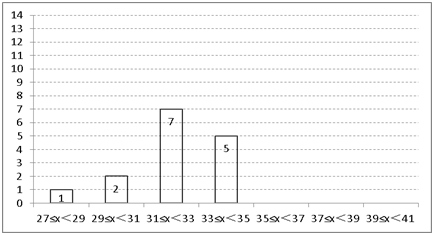
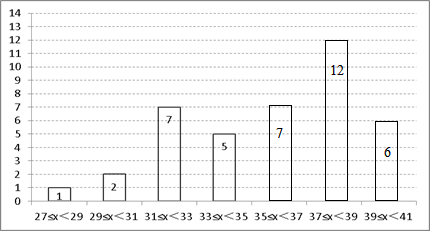
| 年龄段(岁) | 27≤x<29 | 29≤x<31 | 31≤x<33 | 33≤x<35 | 35≤x<37 | 37≤x<39 | 39≤x<41 |
| 频数(人) | 1 | 2 | 7 | 5 | a | b | c |
| 频率 | 0.025 | 0.175 | 0.15 |
| 16 |
| 20 |
| 4 |
| 5 |


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
| A、了解报考军事院校考生的视力 |
| B、旅客上飞机前的安检 |
| C、对招聘教师中的应聘人员进行面试 |
| D、了解全市中小学生每天的零花钱 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 材料板的宽x (单位:cm) |
24 | 30 | 42 | 54 |
| 成本c (单位:元) |
96 | 150 | 294 | 486 |
| 销售价格y (单位:元) |
780 | 900 | 1140 | 1380 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
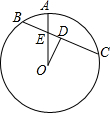 如图,D是⊙O弦BC的中点,A是
如图,D是⊙O弦BC的中点,A是 |
| BC |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40
如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com