Question

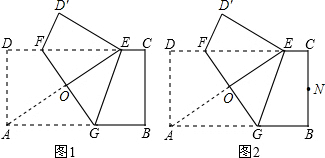
如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．

（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；

（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC的中点；

（3）如图2，在（2）的条件下，求折痕FG的长．

 

Answer 1

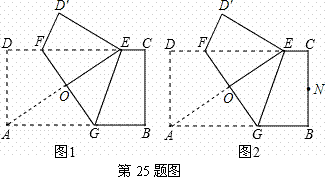【解答】（1）（3分）由折叠的性质可得，GA=GE，∠AGF=∠EGF，

∵DC∥AB，

∴∠EFG=∠AGF，

∴∠EFG=∠EGF，

∴EF=EG=AG，

∴四边形AGEF是平行四边形（EF∥AG，EF=AG），

又∵AG=GE，

∴四边形AGEF是菱形．………………3分

（2）（3分）连接ON，

∵△AED是直角三角形，AE是斜边，点O是AE的中点，△AED的外接圆与BC相切于点N，

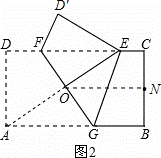∴ON⊥BC，

∵点O是AE的中点，

∴ON是梯形ABCE的中位线，

∴点N是线段BC的中点．………………6分

（3）（4分）解法一：作OM⊥AB于M，则四边形OMBN是矩形。

∴OM＝BN＝BC＝1

令ON＝x，则由（2）得OE＝OA＝ON＝MB＝x（外接圆半径），

∵AM＝AB－MB＝4－x

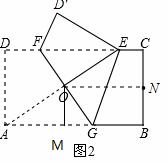在Rt△AOM中，由勾股定理得：OA²＝AM²+OM²

即x²=(4－x)²+1²

解之得：x＝

∴AM＝4－＝

又∵Rt△AOM∽Rt△EFO

∴＝   即＝

∴OF＝    ∴FG＝2OF＝  ………………………………10分

解法二：（4分）延长NO交AD于H，则AH＝BN＝1，NH＝4

令ON＝x，则由（2）得OE＝OA＝ON＝x（外接圆半径），

∵OH＝4－x

在Rt△AOH中，由勾股定理得：OA²＝AH²+OH²

即x²=1² +(4－x)²

解之得：x＝

∴HO＝4－＝

又∵Rt△AOM∽Rt△EFO

∴＝

即：＝

∴OF＝  

 ∴FG＝2OF＝  …………………………………………10分