
【题目】如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时. 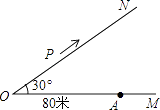
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
【答案】
(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= ![]() BC,OA=80m,
BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= ![]() OA=
OA= ![]() ×80=40m,
×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= ![]() =
= ![]() =30m,
=30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 ![]() =300米/分钟,
=300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
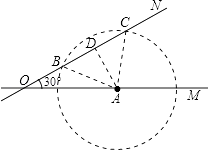
【解析】(1)直接利用直角三角形中30°所对的边等于斜边的一半求出即可;(2)根据题意可知,图中AB=50m,AD⊥BC,且BD=CD,∠AOD=30°,OA=80m;再利用垂径定理及勾股定理解答即可.


科目:初中数学 来源: 题型:
【题目】2008北京奥运会主会场“鸟巢”的座席数是91 000个,这个数用科学记数法表示为( )
A.0.91×105
B.9.1×104
C.91×103
D.9.1×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准是:起步价8元,当路程超过2km时,每1km收费1.8元,如果某出租车行驶x(x>2km),则司机应收费(单位:元)( )
A. 8+1.8(x﹣2)B. 8+1.8xC. 8﹣1.8xD. 8﹣1.8(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= ![]() x与一次函数y=﹣x+7的图象交于点A.
x与一次函数y=﹣x+7的图象交于点A. 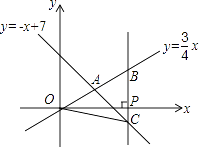
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= ![]() x和y=﹣x+7的图象于点B,C,连接OC.若BC=
x和y=﹣x+7的图象于点B,C,连接OC.若BC= ![]() OA,求△OBC的面积.
OA,求△OBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
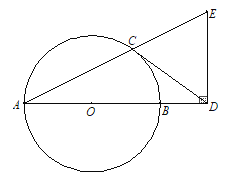
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com