
分析 (1)先移项化为:2x2-3x=-1,再两边除以2,将二次项系数化为1,同加$\frac{9}{16}$进行配方;
(2)化为一般式,计算△,代入求根公式即可;
(3)利用十字相乘分解因式解方程.
解答 解:(1)2x2+1=3x(配方法),
x2-$\frac{3}{2}$x=-$\frac{1}{2}$,
x2-$\frac{3}{2}$x+$\frac{16}{9}$=-$\frac{1}{2}$+$\frac{9}{16}$,
(x-$\frac{3}{4}$)2=$\frac{1}{16}$,
x-$\frac{3}{4}$=±$\frac{1}{4}$,
x1=1,x2=$\frac{1}{2}$;
(2)3x2+5(2x+1)=0(公式法),
3x2+10x+5=0,
△=102-4×3×5=100-60=40,
x=$\frac{-10±\sqrt{40}}{6}$,
x=$\frac{-10±2\sqrt{10}}{6}$,
x=$\frac{-5±\sqrt{10}}{3}$,
x1=$\frac{-5+\sqrt{10}}{3}$,x2=$\frac{-5-\sqrt{10}}{3}$;
(3)用适当的方法解方程:x2-2x-3=0,
(x-3)(x+1)=0,
x-3=0,x+1=0,
x1=3,x2=-1.
点评 本题考查了解一元二次方程,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.这些方法中配方法和公式法适合所有方程,但比较麻烦;用配方法解一元二次方程时要注意:①把原方程要化为ax2+bx+c=0(a≠0)的形式;②二次项系数需化为1,方程两边同时加上一次项系数一半的平方;用公式法解一元二次方程时,必须将原方程化为一般式后,再代入求根公式:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$解方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
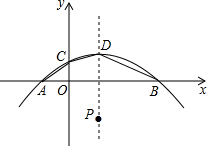 如图,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com