
| AЃЎ | $\left\{\begin{array}{l}{x+y=0}\\{x-y=1}\end{array}\right.$ | BЃЎ | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-1}\end{array}\right.$ | CЃЎ | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ | DЃЎ | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ |
ЗжЮі Аб$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ДњШыИїЗНГЬзщМьбщМДПЩЃЎ
НтД№ НтЃКЗНГЬзщ$\left\{\begin{array}{l}{x+y=0Ђй}\\{x-y=2Ђк}\end{array}\right.$ЃЌ
Ђй+ЂкЕУЃК2x=2ЃЌМДx=1ЃЌ
Ђй-ЂкЕУЃК2y=-2ЃЌМДy=-1ЃЌ
дђвд$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ЮЊНтЕФЖўдЊвЛДЮЗНГЬзщЪЧ$\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ЃЎ
ЙЪбЁDЃЎ
ЕуЦР ДЫЬтПМВщСЫЖўдЊвЛДЮЗНГЬзщЕФНтЃЌЗНГЬзщЕФНтМДЮЊФмЪЙЗНГЬзщжаСНЗНГЬЖМГЩСЂЕФЮДжЊЪ§ЕФжЕЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
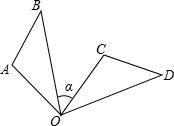 ШчЭМЃЌЁїOABШЦЕуOЫГЪБеыа§зЊ85ЁуЕНЁїOCDЃЌвбжЊЁЯA=110ЁуЃЌШєЁЯD=40ЁуЃЌдђЁЯІСЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌЁїOABШЦЕуOЫГЪБеыа§зЊ85ЁуЕНЁїOCDЃЌвбжЊЁЯA=110ЁуЃЌШєЁЯD=40ЁуЃЌдђЁЯІСЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 30Ёу | BЃЎ | 45Ёу | CЃЎ | 55Ёу | DЃЎ | 60Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | x2-2x=7 | BЃЎ | 3x-y=1 | CЃЎ | xy-4=0 | DЃЎ | x+$\frac{1}{x}$=1 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com