
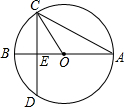
 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=2,CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$ | D. | 4 |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
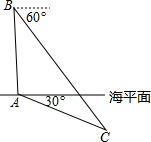 中国与俄罗斯两国海军正在黑海进行联合演习,在演习中我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1600米的反潜直升机B测得潜艇C的俯角为60°,试根据以上数据求出潜艇C离海平面的下潜深度.
中国与俄罗斯两国海军正在黑海进行联合演习,在演习中我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1600米的反潜直升机B测得潜艇C的俯角为60°,试根据以上数据求出潜艇C离海平面的下潜深度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 选手 | 甲 | 乙 | 丙 |
| 平均数 | 9.3 | 9.3 | 9.3 |
| 方差 | 0.026 | 0.015 | 0.032 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com