
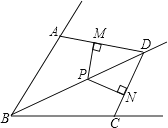
【题目】已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
【答案】(1)见解析 (2)见解析
【解析】
(1)根据角平分线的定义可得∠ABD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可得到答案;
(2)利用“HL”证明Rt△PDM≌Rt△PDN,根据全等三角形对应边相等可得DM=DN,然后根据线段的垂直平分线性质定理的逆定理即可得到结论;
解:(1) ∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
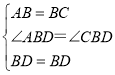 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN(角平分线上的点到角两边的距离相等);
(2)在Rt△PDM和Rt△PDN中,
![]() ,
,
∴Rt△PDM≌Rt△PDN(HL),
∴DM=DN,
∴D在MN的垂直平分线上,
∵PM=PN,
∴P在MN的垂直平分线上,
∴PD是MN的垂直平分线.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】为倡导“低碳生活”,人们现在常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1cm.参考数据:sin75°≈0.966,cos75°≈0.259,tan75°≈3.732).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶.设慢车行驶的时间x(h),两车之的距离为y(km),图中的折线表示y与x之间的函数关系.
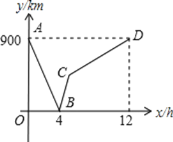
(1)求慢车和快车的速度;
(2)求线段BC所表示的y与x的函数关系式,并写出自变量x的取值范围;
(3)第一列快车出发后又有一列快车(与第一列快车速度相同)从甲地出发,与慢车同时到达各自的目的地.请直接写出第二列快车出发后经过多少小时与慢车相遇,相遇时他们距甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
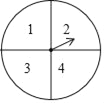
【题目】元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC交BD于P,E为BC上一点,AE交BD于F,若AB=AE,![]() ,则下列结论:①AF=AP;②AE=FD;③BE=AF.正确的是______(填序号).
,则下列结论:①AF=AP;②AE=FD;③BE=AF.正确的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ,
, ![]() )
)
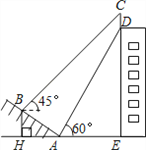
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
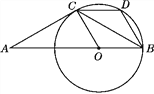
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com