练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    32、操作题
    1、如图1把一个边长为4厘米的正方形剪成四个相同的四个直角三角形，把这四个三角形
    （1）画出拼成梯形的两种拼法（2）画出拼成平行四边形的两种拼法；
    2、度量图2中各角，并填表：（精确到1°）

    （1）∠A，∠B，∠ACB之间有什么关系？
    （2）∠A、∠B、∠ACD之间有什么关系？
    分析：（1）根据梯形与平行四边形的特点进行拼接；
    （2）用量角器进行度量，然后确定数量关系．
    解答：解：1、

    2、根据测量结果可得：
    （1）∠A=∠B∠A+∠B+∠ACB=180°
    （2）∠A+∠B=∠ACD．
    点评：熟记梯形与平行四边形的特点以及三角形的内角和、外角和内角的关系，是解决此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    实验与操作：
    小明是一位动手能力很强的同学，他用橡皮泥做成一个棱长为4cm的正方体．
    （1）如图1所示，在顶面中心位置处从上到下打一个边长为1cm的正方形孔，打孔后的橡皮泥块的表面积为
     
    cm2；
    （2）如果在第（1）题打孔后，再在正面中心位置（如图2中的虚线所示）从前到后打一个边长为1cm的正方形通孔，那么打孔后的橡皮泥块的表面积为
     
    cm2；
    （3）如果把（1）、（2）中的边长为1cm的通孔均改为边长为acm（a≠1）的通孔，能否使橡皮泥块的表面积为118cm2？如果能，求出a，如果不能，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本小题满分10分）

    在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：

    第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；

    第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）

    请解答以下问题：

    1.（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．

    2.（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图：一正方形纸片，根据要求进行多次分割，把它分割成若干个直角三角形．具体操作过程如下：第一次分割：将正方形纸片分成4个全等的直角三角形；第二次分割：将上次得到的直角三角形中的一个再分成4个全等的直角三角形；以后按第二次分割的方法重复进行．

    【小题1】请你设计出两种符合题意的分割方案（分割3次）；
    【小题2】设正方形的边长为a，请你通过对其中一种方案的操作和观察，将第二、第三次分割后所得的最小的直角三角形的面积S填入下表：

    【小题3】在条件（2）下，请你猜想：分割所得的最小直角三角形面积S与分割次数n有什么关系？用数学表达式表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    有一个数学活动，其具体操作过程是：   
    第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开
    （如图1）；
    第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）.

    请解答以下问题：
    【小题1】如图2，若延长MN交线段BC于P，△BMP是什么三角形？请证明你的结论．
    【小题2】在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年九年级第二次模拟考试数学卷 题型：解答题

    （本小题满分10分）

    在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：

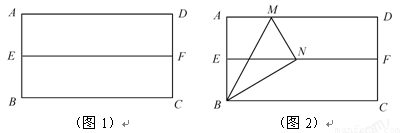
    第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；

    第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）

    请解答以下问题：

    1.（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．

    2.（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？

     

    查看答案和解析>>

    同步练习册答案