
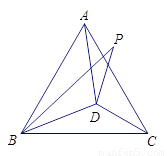
已知:如图,D为等边△ABC内一点,DB=DA,BP=AB,∠DBP=∠DBC,求∠BPD的度数.(10分)
30°
【解析】解:∵△ABC是等边三角形.
∴∠BAC=∠ABC=∠ACB=60°.
AB=AC=BC
又∵DB=DA
∴∠BAD=∠ABD
∴∠BAC-∠BAD=∠ABC-∠ABD
∴∠DAC=∠DBC
在△ADC和△BDC中
DB=DA,∠DBC=∠DAC,AC=BC
∴△ADC≌△BDC(SAS)
∴∠ACD=∠BCD
∴∠BCD=30°
又∵BA=BP
∴BP=BC
在△BPD和△BCD中
BP=BC,∠DBP=∠BCD,BD=BD
∴△BPD≌△BCD(SAS)
∴∠BPD=∠BCD=30°
根据等边三角形的性质先由SSS判定△BCD≌△ACD,从而得到∠BCD=∠ACD= 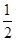 ∠ACB=30°,再利用SAS判定△BDP≌△BDC,从而得到∠P=∠BCD=30°
∠ACB=30°,再利用SAS判定△BDP≌△BDC,从而得到∠P=∠BCD=30°


科目:初中数学 来源: 题型:
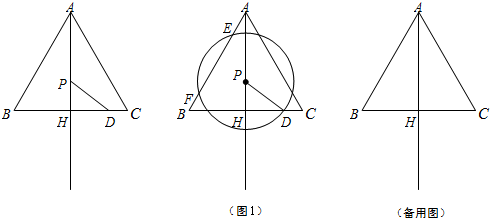
 E,连接CE.
E,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.
已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.查看答案和解析>>
科目:初中数学 来源: 题型:
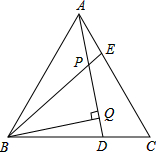 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.
已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com