
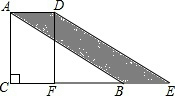
 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
分析 先根据含30度的直角三角形三边的关系得到AC=$\frac{1}{2}$AB=4,则根据平移的性质得AB=DE,AB∥DE,平移的距离等于BE,于是可判断四边形ABED为平行四边形,然后根据平行四边形的面积公式求解.
解答 解:在Rt△ABC中,∵∠ABC=30°,
∴AC=$\frac{1}{2}$AB=4,
∵△ABC沿CB向右平移得到△DEF,
∴AB=DE,AB∥DE,平移的距离等于BE,
∴四边形ABED为平行四边形,
∴BE•AC=12,
∴BE=$\frac{12}{4}$=3.
故选B.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48,43 | B. | 48,48 | C. | 43,48 | D. | 48,49 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
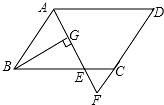 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | a2+b2=(a+b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1<b-1 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | -3a>-3b | D. | $\frac{a}{4}$<$\frac{b}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com