
分析 设增种x棵树,果园的总产量为y千克,列出二次函数关系式,根据二次函数性质求最值即可.
解答 解:设增种x棵树,果园的总产量为y千克
依题意得:
y=(100+x)(60-0.5x)
=6000-50x+60x-0.5x2
=-0.5x2+10x+6000
∵a=-0.5<0,
∴当x=-$\frac{b}{2a}$=-$\frac{10}{2×(-0.5)}$=10时,
y最大值=$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-0.5)×6000-100}{4×(-0.5)}$=6050,
所以增种10棵枇杷树,投产后可以使果园枇杷的总产量最多,最多总产量是6050千克.
点评 本题主要考查了二次函数的应用,根据题意“单颗枇杷树的产量×枇杷树的株数=总产量”列出函数表达式是解决问题的关键.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
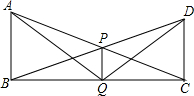 如图,AB、DC都在BC的同侧且AB⊥BC于B,DC⊥BC于C,AC,BD交于点P.PQ⊥BC于Q
如图,AB、DC都在BC的同侧且AB⊥BC于B,DC⊥BC于C,AC,BD交于点P.PQ⊥BC于Q查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com