
分析 化简$\frac{1}{\sqrt{3}-\sqrt{2}}$可得,$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$,由$\sqrt{3}、\sqrt{2}$的值估算出$\sqrt{3}+\sqrt{2}$的整数部分为x=3,故小数部分为y=$\sqrt{3}$+$\sqrt{2}$-3,然后代入所求式子化简即可.
解答 解:∵$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{3}+\sqrt{2}}{3-2}$=$\sqrt{3}$+$\sqrt{2}$,$\sqrt{3}≈1.732,\sqrt{2}≈1.414$.
∴整数部分为x=3,小数部分为y=$\sqrt{3}$+$\sqrt{2}$-3.
∴$\frac{x+2y}{x-2y-4}$
=$\frac{3+2(\sqrt{3}+\sqrt{2}-3)}{3-2(\sqrt{3}+\sqrt{2}-3)-4}$
=$\frac{3+2\sqrt{3}+2\sqrt{2}-6}{3-2\sqrt{3}-2\sqrt{2}+6-4}$
=$\frac{-3+2(\sqrt{3}+\sqrt{2})}{5-2(\sqrt{3}+\sqrt{2})}$
=$\frac{[-3+2(\sqrt{3}+\sqrt{2})]•[5+2(\sqrt{3}+\sqrt{2})]}{[5-2(\sqrt{3}+\sqrt{2})]•[5+2(\sqrt{3}+\sqrt{2})]}$
=$\frac{-15+4(\sqrt{3}+\sqrt{2})+4(\sqrt{3}+\sqrt{2})^{2}}{25-4(\sqrt{3}+\sqrt{2})^{2}}$
=$\frac{5+4(\sqrt{3}+\sqrt{2}+2\sqrt{6})}{5-8\sqrt{6}}$
=$\frac{[5+4(\sqrt{3}+\sqrt{2}+2\sqrt{6})](5+8\sqrt{6})}{(5-8\sqrt{6})(5+8\sqrt{6})}$
=$\frac{25+40\sqrt{6}+20\sqrt{3}+20\sqrt{2}+40\sqrt{6}+96\sqrt{2}+64\sqrt{3}+384}{25-384}$
=$-\frac{409+116\sqrt{2}+84\sqrt{3}+80\sqrt{6}}{359}$.
点评 本题考查二次根式的化简求值和估算无理数的大小的相关知识,本题的关键是对二次根式的化简,要注意分母是无理数的要进行分母有理化.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
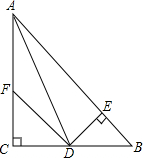 如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明:
如图所示,在△ABC中,DE⊥AB交AB于E,DE=CD,F在AC上,BD=DF,CF=BE,证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
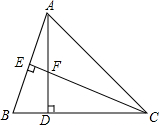 已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.
已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com