

分析 (1)作AG⊥BC,DH⊥BC,垂足分别为G、H,可以得出四边形AGHD为矩形,根据矩形的性质及相关条件可以得出△ABG≌△DCH,可以求出BG=CH的值,再由勾股定理就可以求出AG=DH的值,就可以求出BP的值,即可以求出结论t的值;
(2)先由条件可以求出EF=EQ=PQ-EP=4-$\frac{1}{2}$t,分为三种情况:EF=EP时可以求出t值;当FE=FP时,作FR⊥EP,垂足为R,可以求出t值;当PE=PF时,作PS⊥EF,垂足为S,可以求出t值;即可得出结果.
解答 解:(1)如图2,作AG⊥BC,DH⊥BC,垂足分别为G、H,
∴四边形AGHD为矩形.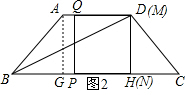
∵梯形ABCD,AB=AD=DC=5,
∴△ABG≌△DCH,
∴BG=$\frac{1}{2}$(BC-AD)=3,AG=4,
∴当正方形PQMN的边MN恰好经过点D时,点M与点D重合,此时MQ=4,
∴GP=AQ=AD-DQ=1,BP=BG+GP=4,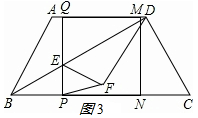
∴t=4,
即4秒时,正方形PQMN的边MN恰好经过点D;
(2)∵∠PEF+∠QEF=180°=∠QDF+∠QEF,
∴∠PEF=∠QDF=2∠ADB=∠ABC,
∴cos∠ABC=cos∠PEF=$\frac{3}{5}$,
由(1)可知EP=$\frac{1}{2}$BP=$\frac{1}{2}$t,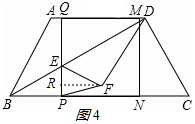
则EF=EQ=PQ-EP=4-$\frac{1}{2}$t,
①如图3,当EF=EP时,4-$\frac{1}{2}$t=$\frac{1}{2}$t,
∴t=4;
②如图4,当FE=FP时,作FR⊥EP,垂足为R,
∴ER=$\frac{1}{2}$EP=$\frac{3}{5}$EF,
∴$\frac{1}{2}$×$\frac{1}{2}$t=$\frac{3}{5}$(4-$\frac{1}{2}$t),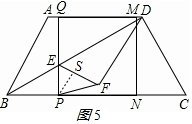
∴t=$\frac{48}{11}$;
③如图5,当PE=PF时,作PS⊥EF,垂足为S,
∵ES=$\frac{1}{2}$EF=$\frac{3}{5}$PE,
∴$\frac{1}{2}$(4-$\frac{1}{2}$t)=$\frac{3}{5}$×$\frac{1}{2}$t,
∴t=$\frac{40}{11}$.
∴当t=4或$\frac{48}{11}$或$\frac{40}{11}$时,△PEF是等腰三角形.
点评 本题是四边形综合题目,考查了动点问题的运用,等腰直角梯形的性质的运用,全等三角形的判定及性质,等腰三角形的性质等知识;本题综合性强,有一定难度,特别是(2)中需要进行分类讨论才能得出结果.


科目:初中数学 来源: 题型:选择题
 三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )| A. | 2πmn | B. | $\frac{1}{2}$πmn | C. | π(m+n) | D. | πmn |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠BAC的角平分线交边BC于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,∠BAC的角平分线交边BC于点D,过点D作DE⊥AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com