
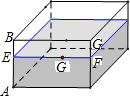
 有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).
有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
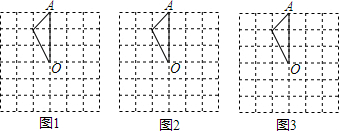
 (1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;
(1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由3x-2=2x+1,移项得3x+2x=2+1 | |
| B. | 由$\frac{x-2}{2}$-$\frac{3x-2}{4}$=-1,去分母得2(x-2)-3x-2=-4 | |
| C. | 由2-3(x-1)=4,去括号得2-3x+3=4 | |
| D. | 由2x+3-x=5,合并同类项得3x+3=5. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
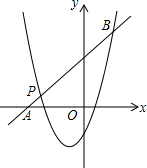 已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.
已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com