
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

【答案】(1)40°;(2)不变化,1:2;(3)60°,理由见解析.
【解析】试题分析:根据两直线平行,同旁内角互补求出∠AOC,然后求出∠EOB=![]() ∠AOC,计算即可得解;
∠AOC,计算即可得解;
(2)根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠OFC=2∠OBC,从而得解;
(3)根据三角形的内角和定理求出∠COE=∠AOB,从而得到OB、OE、OF是∠AOC的四等分线,再利用三角形的内角和定理列式计算即可得解.
试题解析:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=![]() ∠AOC=
∠AOC=![]() ×80°=40°;
×80°=40°;
(2)∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×80°=20°,
×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某地区2016年投入教育经费2500万元,预计2018年投入3600万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )
A.25x2=3600B.2500(1+x)2=3600
C.2500(1+x%)2=3600D.2500(1+x)+ 2500(1+x)2=3600
查看答案和解析>>
科目:初中数学 来源: 题型:
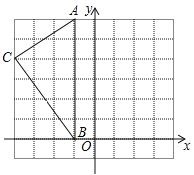
【题目】如图,△ABC在平面直角坐标系的坐标分别为A(﹣1,5),B(﹣1,0),C(﹣4,3),按要求完成:
(1)在同一坐标系中,画出△ABC关于y轴对称的图形△A'B'C';
(2)若CD是△ABC中AB边的中线,E是CD的中点,F是AE的中点,连接AE、BE,FB,则△EFB的面积S= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A. 点O在AC的垂直平分线上
B. △AOB、△BOC、△COA都是等腰三角形
C. ∠OAB+∠OBC+∠OCA=90°
D. 点O到AB、BC、CA的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
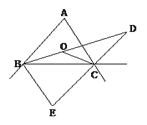
【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )
A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com