
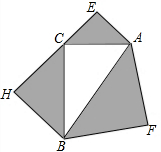
 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
分析 根据题意和图形得到AB2=AC2+BC2,根据勾股定理的逆定理得到∠ACB=90°,根据题意求出AC、BC的长,根据三角形的面积计算即可.
解答 解:∵S△AFB=S△AEC+S△CHB,
∴$\frac{1}{4}$AB2=$\frac{1}{4}$AC2+$\frac{1}{4}$BC2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∵$\frac{1}{4}$AC2=25,$\frac{1}{4}$BC2=144,
∴AC=10,BC=24,
∴S△ACB=$\frac{1}{2}$×10×24=120,
故选:B.
点评 本题考查的是勾股定理的逆定理的应用,勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
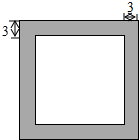 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?
一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
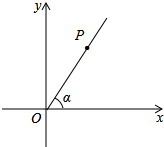 如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$
如图,点P是∠α的边OA上的一点,已知点P的横坐标为6,若sinα=$\frac{4}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
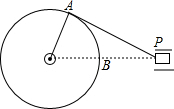 如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.
如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
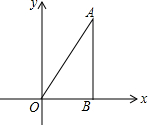 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com