
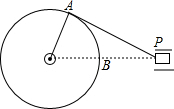
 如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.
如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
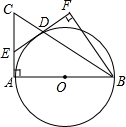 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
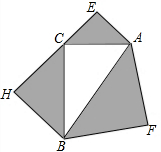 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
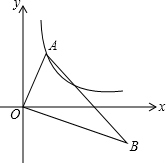 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com