
【题目】如图,∠ABC=∠ACB,AD、BD分别平分△ABC的外角∠EAC、内角∠ABC,以下结论:① AD∥BC;②∠ACB=2∠ADB;③ BD⊥AC;④ AC=AD.其中正确的结论有( )

A.①②B.①②④C.①②③D.①③④
【答案】B
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质进而解答即可.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵BD平分∠ABC,∠ABC=∠ACB,
∵∠ABC+∠ACB+∠BAC=180°,
当∠BAC=∠C时,才有∠ABD+∠BAC=90°,故③错误;
∵∠ADB=∠ABD,
∴AD=AB,
∴AD=AC,故④正确;
故选:B.


科目:初中数学 来源: 题型:
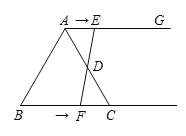
【题目】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动;同时点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s).
(1)△ABC的BC边上的高为_________cm;
(2)连接EF,当EF经过AC的中点D时,求证:△ADE≌△CDF;
(3)求当t为何值时,AC与EF互相平分;
(4)当t=________s时,四边形ACFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:![]() .
.
解:讨论:①当![]() ≥0时,原方程可化为
≥0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
②当![]() <0时,原方程可化为
<0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
∴原方程的解为![]() 和
和![]() .
.
问题(1):依例题的解法,方程![]() 的解是 ;
的解是 ;
问题(2):尝试解绝对值方程:![]() ;
;
问题(3):在理解绝对值方程解法的基础上,解方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
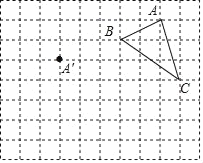
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com