
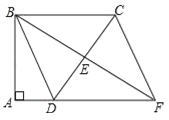
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
【答案】(1)证明见解析;(2)![]() cm2或
cm2或![]() cm2.
cm2.
【解析】
试题分析:(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;
(2)分三种情况:①BC=BD时,由勾股定理列式求出AB,由平行四边形的面积公式列式计算即可得解;
②BC=CD时,过点C作CG⊥AF于G,证出四边形AGCB是矩形,由矩形的对边相等得AG=BC=3,求出DG=2,由勾股定理列式求出CG,由平行四边形的面积列式计算即可;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.
试题解析:(1)证明:∵∠A=∠ABC=90°,∴BC∥AD,∴∠CBE=∠DFE,在△BEC与△FED中,∵∠CBE=∠DFE,∠BEC=∠FED,CE=DE,∴△BEC≌△FED(AAS),∴BE=FE,又∵E是边CD的中点,∴CE=DE,∴四边形BDFC是平行四边形;
(2)解:分三种情况:①BC=BD=30cm时,由勾股定理得,AB=![]() =
=![]() =
=![]() (cm),∴四边形BDFC的面积=
(cm),∴四边形BDFC的面积=![]() =
=![]() (cm2);
(cm2);
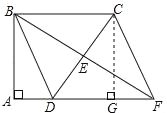
②BC=CD=30时,过点C作CG⊥AF于G,如图所示:
则四边形AGCB是矩形,∴AG=BC=30,∴DG=AG﹣AD=30﹣10=20,由勾股定理得,CG=![]() =
=![]() =
=![]() ,∴四边形BDFC的面积=
,∴四边形BDFC的面积=![]() =
=![]() ;
;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=20,矛盾,此时不成立;
综上所述,四边形BDFC的面积是![]() cm2或
cm2或![]() cm2.
cm2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
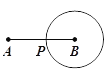
【题目】如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
A. 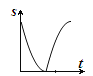 B.
B. 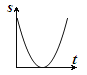 C.
C. 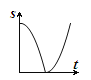 D.
D. 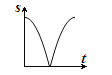
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 以下调查中适合作抽样调查的有( ).
① 了解全班同学期末考试的数学成绩情况; ② 了解夏季冷饮市场上冰淇淋的质量情况;③ 学校为抗击“非典”,需了解全校师生的体温; ④ 了解《课课练》在全省七年级学生中受欢迎的程序.
A. 1个 B. 2个 C. 3个 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个. 求:
(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com