
分析 (1)模仿例题,即可得出结论.
(2)设四位对称数分解为前两位数所表示的数为:10a+b,和后两位数所表示的数为10b+a,用a、b的代数式表示这两个数的差即可解决问题.
(3)设这个三位对称数为:100a+10b+a,由题意100a+10b+a-(2a+b)=99a+9b=11(9a+$\frac{9b}{11}$),根据整除的定义,即可解决问题.
解答 解:(1)678+876=1473,1473+3741=5214,5214+4152=9339,
所以以678产生的第一个对称数是9339.
(2)设四位对称数分解为前两位数所表示的数为:10a+b,
和后两位数所表示的数为10b+a,
由题意(10a+b)-(10b+a)=9a-9b=9(a-b),
∵a、b为整数,
∴(a-b)是整数,
∴9(a-b)一定能被9整除,
∴这两个数的差一定能被9整除.
(3)设这个三位对称数为:100a+10b+a,
由题意100a+10b+a-(2a+b)=99a+9b=11(9a+$\frac{9b}{11}$),
∵所得的结果能被11整除,
∴9a+$\frac{9b}{11}$为整数,
∵a、b为整数,且0≤b≤9,1≤a≤9,
∴$\frac{9b}{11}$为整数,
∴b=0,a有9种可能,
∴满足条件的三位对称数共有9个.
点评 本题考查因式分解的应用、数字问题等知识,解题的关键是理解题意,学会利用参数解决问题,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“等腰线段”.
我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“等腰线段”.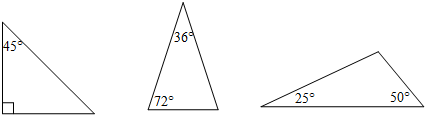

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )
如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm,若水面上升2cm(即EG=2cm),则此时水面宽AB为( )| A. | 8$\sqrt{3}$cm | B. | 16$\sqrt{3}$cm | C. | 8cm | D. | 16cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com