
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)用配方法将y=2x2﹣4x﹣6化成y=a (x﹣h)2+k的形式;并写出对称轴和顶点坐标.
(2)当0<x<4时,求y的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积.
【答案】
(1)解:y=2x2﹣4x﹣6=2(x2﹣2x+1﹣1)﹣6=2(x2﹣2x+1)﹣2﹣6=2(x﹣1)2﹣8,
∴抛物线的对称轴为x=1,顶点坐标为(1,﹣8)
(2)解:当x=1时,y有最小值,最小值为﹣8,
∵0<x<4,
∴y的最大值为10.
∴y的取值范围是﹣8≤y<10
(3)解:当x=0时,y=﹣6,
当y=0时,2x2﹣4x﹣6=0,解得:x=3或x=﹣1,
∴函数图象与两坐标轴交点所围成的三角形的面积= ![]() ×4×6=12
×4×6=12
【解析】(1)可利用配方法配成顶点式;(2)数形结合,在0<x<4内求出最小值与最大值;(3)需分别令x=0、y=0求出抛物线与y、x轴的交点坐标代入公式即可.
【考点精析】本题主要考查了二次函数的性质和抛物线与坐标轴的交点的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
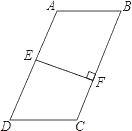
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年端午节前夕,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
商品 单价(元/件) | 成本价 | 销售价 |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
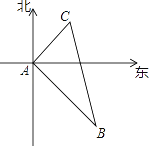
【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
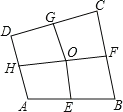
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com