
 如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.
如图,已知抛物线y=x2-2tx+t2-2的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线与点P.分析 (1)把解析式转化成顶点式,得出顶点坐标,进而根据已知得出A(2,-2),从而得出抛物线的解析式,把x=1代入即可求得P的坐标;
(2)根据已知得出三角形ABE是等腰直角三角形,得出BE=AB=t,即E(0,-2+t),根据待定系数法求得AE的解析式,然后和抛物线的解析式联立方程,解方程即可求得P(t-1,-1),然后根据梯形的面积公式即可求得;
(3)根据已知得出$\frac{1}{2}$PD•t=2(-$\frac{1}{2}$t2-2t+$\frac{3}{2}$),即$\frac{1}{2}$t=t2+4t-3,解方程即可求得.
解答 解:(1)∵抛物线y=x2-2tx+t2-2=(x-t)2-2,
∴顶点A(t,-2),
∵点C的横坐标为1,且是线段AB的中点,
∴$\frac{t}{2}$=1,
∴t=2,
∴A(2,-2),
∴抛物线的解析式为y=(x-2)2-2=x2-4x+2,
当x=1时,y=1-4+2=-1,
∴P(1,-1);
(2)当AC=CP时,∠EAB=45°,
∴BE=AB=t,即E(0,-2+t),
∴直线AE的解析式为y=-x+t-2,
由$\left\{\begin{array}{l}{y=-x+t-2}\\{y={x}^{2}-2tx+{t}^{2}-2}\end{array}\right.$得P(t-1,-1),
∴S=$\frac{1}{2}$OD×(OE+DP)=$\frac{1}{2}$(t-1)×(-t+2+1),
∴S=-$\frac{1}{2}$t2+2t-$\frac{3}{2}$(1<t<2);
(3)∵S△ADE=2S,
∴$\frac{1}{2}$PD•t=2(-$\frac{1}{2}$t2-2t+$\frac{3}{2}$),即$\frac{1}{2}$t=t2+4t-3,
解得t=2(舍去)或t=$\frac{3}{2}$.
点评 本题是二次函数的综合题,考查了待定系数法求解析式,抛物线的顶点以及抛物线和直线的交点,梯形的面积,三角形的面积等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
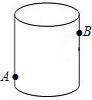 如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.
如图,圆柱形玻璃容器高20cm,底面圆的周长为48cm,在外侧距下底1cm的点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度为30cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,-1) | B. | (-2,1) | C. | (1,-2) | D. | (-1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
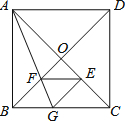 如图,在正方形ABCD中,AC、BD相交于点O,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AG交BD于点F,连结EG、EF.下列结论:
如图,在正方形ABCD中,AC、BD相交于点O,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AG交BD于点F,连结EG、EF.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
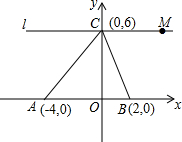 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
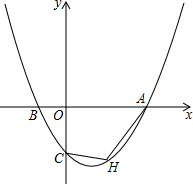 如图,已知抛物线y=ax2+bx+c过点A(6,0),B(-2,0),C(0,-3).
如图,已知抛物线y=ax2+bx+c过点A(6,0),B(-2,0),C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
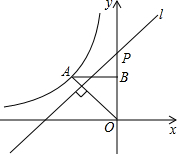 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com