
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 . 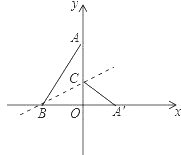
【答案】(0,![]() )
)
【解析】∵A(0,4),B(-3,0),
∴OA=4,OB=3,
在Rt△OAB中,AB= ![]() ,
,
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=5,CA′=CA,
∴OA′=BA′-OB=5-3=2,
设OC=t,则CA=CA′=OA-OC=4-t,
在Rt△OA′C中,由勾股定理得:OC2+OA′2=CA′2,
即t2+22=(4-t)2,
解得:t= ![]() ,
,
∴C点坐标为(0, ![]() ).
).
【考点精析】通过灵活运用勾股定理的概念和翻折变换(折叠问题),掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )

A. 6![]() B. -6
B. -6![]() C. 12
C. 12![]() D. -12
D. -12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
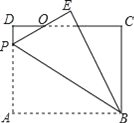
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).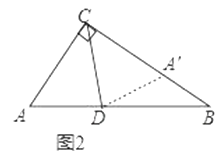
请回答:
(1)在图2中,小明得到的全等三角形是△≌△;
(2)求BC和AC、AD之间的数量关系是
(3)参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.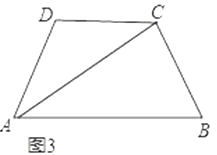
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com