
 如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.
如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.| DF |
| CF |
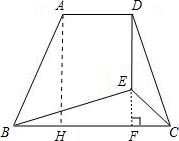 解:(1)延长DE交BC于F,
解:(1)延长DE交BC于F,
|
| 3+x |
| x |
| 3+x |
| x |
| DF2+CF2 |
| 42+12 |
| 17 |
| 17 |
| 17 |
|
| 17 |
| 17 |
| 17 |


科目:初中数学 来源: 题型:
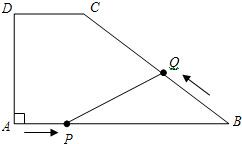 发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论.
(2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论.| AE |
| EB |
| 1 |
| 3 |
| AE |
| EB |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com