
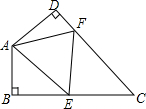
 如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 据要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=50°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.
解答 解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,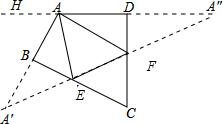
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′E+∠A″=∠HAA′=50°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=50°,
∴∠EAF=130°-50°=80°,
故选:D.
点评 本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出E,F的位置是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
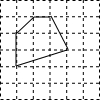 如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.
如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式S=a+$\frac{1}{2}$b-1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克定理”.现用一张方格纸共有200个格点,画有一个格点多边形,它的面积S=40.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( )
如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
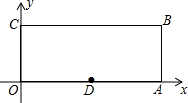 如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).
如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.7×106 | B. | 3.7×105 | C. | 37×104 | D. | 3.7×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com