

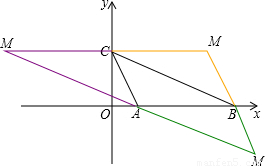
 (1)本题的关键是求出C点的坐标,根据∠OCA=∠OBC易证得三角形OAC与三角形OCB相似,可得出OC2=OA•OB,由此可求得OC的长,即可得出C点的坐标,然后将A、B、C三点坐标代入抛物线中即可求出该二次函数的解析式.
(1)本题的关键是求出C点的坐标,根据∠OCA=∠OBC易证得三角形OAC与三角形OCB相似,可得出OC2=OA•OB,由此可求得OC的长,即可得出C点的坐标,然后将A、B、C三点坐标代入抛物线中即可求出该二次函数的解析式. 解:(1)∵∠AOC=∠COB,∠OCA=∠OBC
解:(1)∵∠AOC=∠COB,∠OCA=∠OBC
 x2-
x2- x+4
x+4

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2010年上海市宝山区罗店中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年福建省漳州市双语实验学校自主招生考试数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年上海市徐汇区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com