
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD+AB,∠BAC=45°,E是BC上一点,且∠DAE=45°,若BC=8,则△ADE面积为__.

【答案】![]()
【解析】
过点A作CD的垂线,交CD的延长线于点F,可得四边形ABCF是正方形,设CD=m,根据勾股定理可求出m=2,将△ABE绕点A顺时针旋转90°至△AFG,可以证明△ADE≌△ADG,设BE=n,再根据勾股定理可求DG的长,进而可得△ADG的面积,即可得△ADE的面积.
解:如图,过点A作CD的垂线,交CD的延长线于点F,

![]() ,
,
![]() ,
,
![]() .
.
![]()
∴四边形ABCF是矩形.
∵∠ABC=90°,∠BAC=45°,
∴AB=BC,
∴四边形ABCF是正方形,
∴AB=BC=AF=CF=8,
设CD=m,
则AD=CD+AB=m+8,DF=CF﹣CD=8﹣m,
在Rt△AFD中,根据勾股定理,得
(m+8)2=(8﹣m)2+82,
解得m=2,
∴FD=6,AD=10,
将△ABE绕点A顺时针旋转90°至△AFG,
∴AG=AE,BE=FG,∠EAG=∠BAF=90°,
∵∠BAC=45°,∠DAE=45°,
∴∠BAE=∠DAC,
∴∠CAE=∠DAF,
∵∠BAE=∠FAG,
∴∠DAE=∠DAG,
AD=AD,
∴△ADE≌△ADG(SAS),
∴DE=DG,
设BE=n,则CE=BC﹣BE=8﹣n,DE=DG=DF+FG=DF+BE=6+n,
在Rt△DCE中,根据勾股定理,得
(6+n)2=(8﹣n)2+22
解得n=![]() ,
,
∴DG=6+![]() =
=![]() ,
,
∴S△ADE=S△ADG=![]() DG×AF=
DG×AF=![]() ×8=
×8=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,反映的是九(1)班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图,下列说法:①九(1)班外出步行有8人;②在圆形统计图中,步行人数所占的圆心角度数为82°;
③九(1)班外出的学生共有40人;④若该校九年级外出的学生共有500人,那么估计全年级外出骑车的人约有150人,其中正确的结论是( )


A. ①②③ B. ①③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:

(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
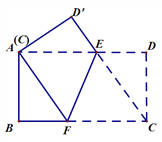
【题目】如图,将矩形ABCD折叠,使C点与A点重合,折痕为EF.
(1)判断四边形AFCE的形状,并说明理由;
(2)若AB=4,BC=8,求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )

A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对称变换和平移变换在平面几何中有着广泛的应用,特别是在解决有关最值问题时,更是我们常用的思维方法,请你利用所学知识解决下列问题:

(1)如图①,在平面直角坐标系中,已知点A(0,1),点B(2,1),点P在x轴上运动,当PA+PB的值最小时,点P的坐标是 ;(请直接写出答案)
(2)如图②,AD⊥l于点D,BC⊥l于点C,且AD=2,AB=BC=4,当点P在直线l上运动时,PA+PB的最小值是 ;(请直接写出答案)
(3)如图③,直线a∥b,且a与b之间的距离为1,点A到直线a的距离为2,点B到直线b的距离为2,且AB=![]() ,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
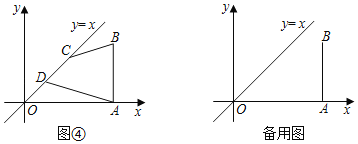
(4)如图④,在平面直角坐标系中,A(6,0),B(6,4),线段CD在直线y=x上运动,且CD=2![]() ,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,联结
,联结![]() 、
、![]() ,若
,若![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() .
.

(1)求线段![]() 的长;
的长;
(2)联结![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表如下:

零花钱数额(元) | 5 | 10 | 15 | 20 |
学生个数(个) | a | 15 | 20 | 5 |
请根据表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的众数、中位数和平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com