
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且=.
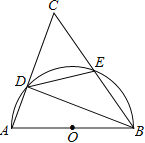
(1)试判断△ABC的形状,并说明理由.
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
【答案】(1)△ABC为等腰三角形;理由见解析;(2)![]() .
.
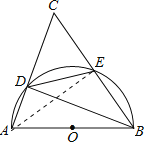
【解析】试题分析:(1)连结AE,如图,根据圆周角定理,由=得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
(2)由等腰三角形的性质得BE=CE=BC=6,再在Rt△ABE中利用勾股定理计算出AE=8,接着由AB为直径得到∠ADB=90°,则可利用面积法计算出BD=![]() ,然后在Rt△ABD中利用勾股定理计算出AD=
,然后在Rt△ABD中利用勾股定理计算出AD=![]() ,再根据正弦的定义求解.
,再根据正弦的定义求解.
解:(1)△ABC为等腰三角形.理由如下:
连结AE,如图,
∵=,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴BE=CE=BC=×12=6,
在Rt△ABE中,∵AB=10,BE=6,
∴AE=![]() =8,
=8,
∵AB为直径,
∴∠ADB=90°,
∴AEBC=BDAC,
∴BD=![]() =
=![]() ,
,
在Rt△ABD中,∵AB=10,BD=![]() ,
,
∴AD=![]() =
=![]() ,
,
∴sin∠ABD=![]() =
=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
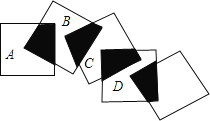
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )
A、这组数据的平均数是84;
B、这组数据的众数是85;
C、这组数据的中位数是84;
D、这组数据的方差是36.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.

(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
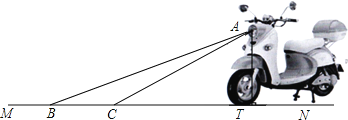
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠C=![]() ,∠EAC+∠FBC=
,∠EAC+∠FBC=![]()
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则![]() 与
与![]() 有何关系?并说明理由.
有何关系?并说明理由.

(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与![]() 、
、![]() 的关系是 .(用
的关系是 .(用![]() 、
、![]() 表示)
表示)

(3)如图③,若![]() ≥
≥![]() ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于![]() ,
, ![]() ;依此类推,则
;依此类推,则![]() = (用
= (用![]() 、
、![]() 表示)
表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
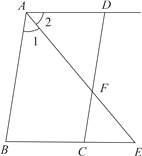
∵AB∥DC(已知)
∴∠1=∠CFE( )
∵AE平分∠BAD(已知)
∴∠1= ∠2 (角平分线的定义)
∵∠CFE=∠E(已知)∴∠2= (等量代换)
∴AD∥BC( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com