
����Ŀ����ƽ��ֱ������ϵxOy�У���֪�����ߵĶ�������Ϊ��2��0�����Ҿ����㣨4��1������ͼ��ֱ��y=![]() x�������߽���A��B���㣬ֱ��lΪy=��1��
x�������߽���A��B���㣬ֱ��lΪy=��1��
��1���������ߵĽ���ʽ��
��2����l���Ƿ����һ��P��ʹPA+PBȡ����Сֵ�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3��֪F��x0��y0��Ϊƽ����һ���㣬M��m��n��Ϊ��������һ���㣬�ҵ�M��ֱ��l�ľ������M����F�ľ���������ȣ���F�����꣮

���𰸡���1�������ߵĽ���ʽΪy=![]() x2��x+1����2����P������Ϊ��
x2��x+1����2����P��������![]() ����1������3������F��������2��1����
����1������3������F��������2��1����
����������1���������ߵĶ�������Ϊ��2��0�������������ߵĽ���ʽΪy=a��x-2��2���������߹��㣨4��1�������ô���ϵ����������������ߵĽ���ʽ��
��2������ֱ��AB�������߽���ʽ�ɷ����飬ͨ���ⷽ����������A��B�����꣬����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ�����ݵ�B������ɵó���B������꣬���ݵ�A��B����������ô���ϵ���������ֱ��AB��Ľ���ʽ��������һ�κ���ͼ���ϵ�������������������P�����ꣻ
��3���ɵ�M��ֱ��l�ľ������M����F�ľ���������Ƚ�϶��κ���ͼ���ϵ���������������ɵó���1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0����m�������Կɵó�����x0��y0�ķ����飬��֮�����������F�����꣮
��1���������ߵĶ�������Ϊ��2��0����
�������ߵĽ���ʽΪy=a��x-2��2��
�߸������߾����㣨4��1����
��1=4a����ã�a=![]() ��
��
�������ߵĽ���ʽΪy=![]() ��x-2��2=
��x-2��2=![]() x2-x+1��
x2-x+1��
��2������ֱ��AB�������߽���ʽ�ɷ����飬�ã�
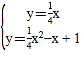 ����ã�
����ã�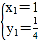 ��
��![]() ��
��
���A��������1��![]() ������B��������4��1����
������B��������4��1����
����B����ֱ��l�ĶԳƵ�B�䣬����AB�佻ֱ��l�ڵ�P����ʱPA+PBȡ����Сֵ����ͼ1��ʾ����

�ߵ�B��4��1����ֱ��lΪy=-1��
���B���������4��-3����
��ֱ��AB��Ľ���ʽΪy=kx+b��k��0����
��A��1��![]() ����B�䣨4��-3������y=kx+b���ã�
����B�䣨4��-3������y=kx+b���ã�
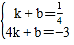 ����ã�
����ã�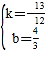 ��
��
��ֱ��AB��Ľ���ʽΪy=-![]() x+
x+![]() ��
��
��y=-1ʱ����-![]() x+
x+![]() =-1��
=-1��
��ã�x=![]() ��
��
���P��������![]() ��-1����
��-1����
��3���ߵ�M��ֱ��l�ľ������M����F�ľ���������ȣ�
�ࣨm-x0��2+��n-y0��2=��n+1��2��
��m2-2x0m+x02-2y0n+y02=2n+1��
��M��m��n��Ϊ��������һ���㣬
��n=![]() m2-m+1��
m2-m+1��
��m2-2x0m+x02-2y0��![]() m2-m+1��+y02=2��
m2-m+1��+y02=2��![]() m2-m+1��+1��
m2-m+1��+1��
�������1-![]() -
-![]() y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
y0��m2+��2-2x0+2y0��m+x02+y02-2y0-3=0��
��mΪ����ֵ��
�� ��
��
��![]() ��
��
�ඨ��F������Ϊ��2��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
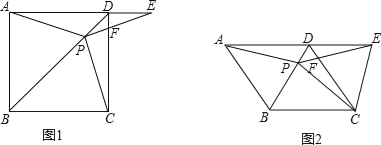
����Ŀ����ͼ1����������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F��
��1��֤����PC=PE��
��2������CPE�Ķ�����
��3����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ������CE����̽���߶�AP���߶�CE��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У�AD�ǡ�BAC�Ľ�ƽ���ߣ���AB=AC+CD.��ô��ACB ���ABC��������������ϵ? С��ͨ���۲�������γ������½���˼·:

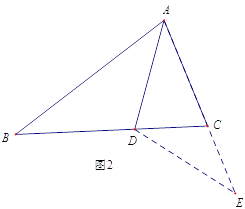
��ͼ2,�ӳ�AC��E,ʹCE=CD,����DE,��AB=AC+CD,�ɵ�AE=AB,����ΪAD�ǡ�BAC��ƽ���ߣ��ɵ���ABD�ա�AED,��һ�������Ϳ��Եõ���ACB ���ABC��������ϵ.
(1) �ж���ABD ����AED ȫ�ȵ�������______________(SSS,SAS,ASA,AAS ������ѡ��һ��);
(2)��ACB ���ABC��������ϵΪ:___________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
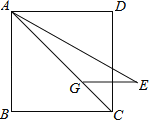
����Ŀ����ͼ��������ABCD�У���GΪ�Խ���AC��һ�㣬AG=AB����CAE=15����AE=AC������GE�����߶�AE�Ƶ�A��ʱ����ת�õ��߶�AF��ʹDF=GE�����CAF�Ķ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ֽƬABC����A��80������D��AC����һ�㣬��BD�������������ֽƬ������������ֽƬ��Ϊ���������Σ�����C�Ķ���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ����������
����������![]() ��
��![]() ����
����
��1����˵����![]() ��
��![]() ��һ�κ�����
��һ�κ�����
��2����![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��������ϵʽ��
��������ϵʽ��
��3������2�������õĺ���ͼ��ƽ�ƣ�ʹ������![]() ����ƽ�ƺ��ֱ�ߵĽ���ʽ��
����ƽ�ƺ��ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��

��1������![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ����д��
����д��![]() ����������ꣻ
����������ꣻ
��2����![]() ����ƽ��6����λ������ƽ�ƺ��
����ƽ��6����λ������ƽ�ƺ��![]() ��д��
��д��![]() ����������ꣻ
����������ꣻ
��3���۲�![]() ��
��![]() �������Ƿ����ijֱ�߶Գƣ����ǣ����ô����������Գ��ᣮ
�������Ƿ����ijֱ�߶Գƣ����ǣ����ô����������Գ��ᣮ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(9��)��ͼ����ƽ��ֱ������ϵ����Rt��ABC����������ֱ���A(��3��2)��B(0��4)��C(0��2)��
(1)����ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ����A1B1C��ƽ����ABC����A�Ķ�Ӧ��A2������Ϊ(0��4)������ƽ�ƺ��Ӧ����A2B2C2��
(2)������A1B1C��ijһ����ת���Եõ���A2B2C2����ֱ��д����ת���ĵ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
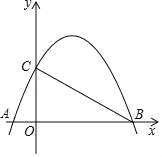
����Ŀ����ͼ����ֱ֪��y=��![]() x+2��x�ᡢy��ֱ��ڵ�B��C��������y=��
x+2��x�ᡢy��ֱ��ڵ�B��C��������y=��![]() +bx+c����B��C������x�ύ����һ����A��
+bx+c����B��C������x�ύ����һ����A��
��1����������ߵı���ʽ��
��2����M���߶�BC��һ�㣬����M��ֱ��l��y�ύ���������ڵ�N�����ı���OMNC��ƽ���ı���ʱ�������������
��3������AC�����D�Ǹ��������ϵ�һ�㣬�������DBA=��CAO�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com