
分析 根据二次根式的性质和完全平方公式把原式化简,代入计算即可.
解答 解:当xy=3,x+y=-4时,
x$\sqrt{\frac{x}{y}}$+y$\sqrt{\frac{y}{x}}$=$\frac{x}{y}\sqrt{xy}$+$\frac{y}{x}\sqrt{xy}$
=$\frac{{x}^{2}+{y}^{2}}{xy}\sqrt{xy}$
=$\frac{(x+y)^{2}-2xy}{xy}\sqrt{xy}$
=$\frac{16-6}{3}\sqrt{3}$
=$\frac{10}{3}\sqrt{3}$.
点评 本题考查的是二次根式的化简求值,掌握二次根式的性质、完全平方公式是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 600米 | B. | 800米 | C. | 1000米 | D. | 1300米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+7)和+(-7) | B. | -(-7)与7 | C. | -|-1$\frac{1}{5}$|与-(-$\frac{6}{5}$) | D. | +(-$\frac{1}{100}$)与+(-0.01) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
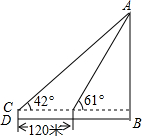 如图,为了测得电视塔的高度AB,在D处用高为1.2米的测角仪CD,测得电视塔顶端A的仰角为42°,再向电视塔方向前进120米,又测得电视塔顶端A的仰角为61°,求这个电视塔的高度AB.(精确到1米)
如图,为了测得电视塔的高度AB,在D处用高为1.2米的测角仪CD,测得电视塔顶端A的仰角为42°,再向电视塔方向前进120米,又测得电视塔顶端A的仰角为61°,求这个电视塔的高度AB.(精确到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com